布线问题

广度搜索问题

问题描述

印刷电路板将布线区域划分成 n×m 个方格如图 a 所示。精确的电路布线问题要求确定连接方格 a 的中点到方格 b 的中点的最短布线方案。在布线时，电路只能沿直线或直角布线，如图 b 所示。为了避免线路相交，已布了线的方格做了封锁标记，其它线路不允穿过被封锁的方格。

img

一个布线的例子：图中包含障碍。起始点为 a，目标点为 b。

img

算法思想

解此问题的队列式分支限界法从起始位置 a 开始将它作为第一个扩展结点。与该扩展结点(a)相邻并且可达的方格成为可行结点被加入到活结点队列中，并且将这些方格标记为 1，即从起始方格 a 到这些方格的距离为 1。

接着，算法从活结点队列中取出队首结点作为下一个扩展结点，并将与当前扩展结点相邻且未标记过的方格标记为 2（表示从起始位置到这个方格距离为2）并存入活结点队列。这个过程一直继续到算法搜索到目标方格 b 或活结点队列为空时为止。即加入剪枝的广度优先搜索。

本质上是广度优先搜索

  • 输入地图后，需要设置上下、左右边界为-1表示墙
  • 判断地图某个点能否走的标准：arr[x][y]==0?
  • 如果到达终点可以提前结束，否则将下个点在地图上标记为上个点的值+1 a[nextX][nextY] = a[now.X][now.Y] + 1，表示距离起点又远了一个单位，并将下个点入队

​

输入

7 7
2 1 3 5
0 0 -1 0 0 0 0
0 0 -1 -1 0 0 0
0 0 0 0 -1 0 0
0 0 0 -1 -1 0 0
-1 0 0 0 -1 0 0
-1 -1 -1 0 0 0 0
-1 -1 -1 0 0 0 0

输出

3 2 -1 0 0 0 0
2 1 -1 -1 0 0 0
1 a 1 2 -1 0 0
2 1 2 -1 -1 b 0
-1 2 3 4 -1 8 0
-1 -1 -1 5 6 7 8
-1 -1 -1 6 7 8 0

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
#include <iostream>
#include <queue>
#include<cstdio>
using namespace std;

int the_start[2]={0,0},the_end[2]={0,0},st, en,n,m,a[40][40], mark[40][40] = {0},direction[4][2] = {0, 1, 0, -1, 1, 0, -1, 0};
queue<pair<int, int> > q;

/*
    功能：打印矩阵测试
*/
void displayMetrix(){
    for (int i = 0; i <= n+1; i++)
    {
        for (int j = 0; j <= m+1; j++)
        {
            printf("%3d",a[i][j]);
        }
        cout<<endl;
    }
}

void print()
{
    for (int i = 1; i <= n; i++)
    {
        for (int j = 1; j <= m; j++)
        {
            if (i == the_start[0] && j == the_start[1])
            {
                cout << "  a";
            }
            else if (i == the_end[0] && j == the_end[1])
            {
                cout << "  b";
            }
            else if (a[i][j] == -1)
            {
                printf("%3d", -1);
            }
            else
            {
                if (a[the_end[0]][the_end[1]] > a[i][j] || a[the_end[0]][the_end[1]] == 0)
                    if (a[i][j])
                        printf("%3d", a[i][j]);
                    else
                        printf("%3d", 0);
                else
                    printf("%3d", 0);
            }
        }
        cout << "\n";
    }
}
int main()
{
    //输入长度，宽度，起点，终点
    cin >> n >> m >> the_start[0] >> the_start[1] >> the_end[0] >> the_end[1];
    the_start[0]++;the_start[1]++;the_end[0]++;the_end[1]++;
    //输入地图
    for (int i = 1; i <= n; i++)
    {
        for (int j = 1; j <= m; j++)
        {
            cin >> a[i][j];
        }
    }
    //设置左右边界，让边界点变成-1
    for(int i=0;i<=n+1;i++){
        a[i][0]=a[i][m+1]=-1;
    }
    //设置上下边界，让边界点变成-1
    for(int i=0;i<=m+1;i++){
        a[0][i]=a[n+1][i]=-1;
    }
    //将起点入队列
    q.push({the_start[0], the_start[1]});
    //标记起点为0
    a[the_start[0]][the_start[1]] = 0;
    //当队列不为空时
    while (!q.empty())
    {
        //依次出队队首
        pair<int, int> now = q.front();
        q.pop();
        int nextX, nextY;
        //从四个方向上进行遍历
        for (int i = 0; i < 4; i++)
        {
            //分别为x和y坐标
            nextX = now.first + direction[i][0];
            nextY = now.second + direction[i][1];
            //如果在界限范围内，并且要求这个位置没走过
            if (a[nextX][nextY] == 0)
            {
                //表示距离起点又远了一个单位
                a[nextX][nextY] = a[now.first][now.second] + 1;
                //如果到达终点提前结束
                if(nextX==the_end[0]&&nextY==the_end[1])
                    break;
                //入队
                q.push({nextX, nextY});
            }
        }
        //提前结束
        if(nextX==the_end[0]&&nextY==the_end[1])
            break;
    }
    print();
}

三维迷宫

题目

公主被魔王抓走了，关押在一个城堡，城堡是ABC的立方体。公主被关在(0,0,0)的位置,离开城堡的出口在(A-1,B-1,C-1)的位置。有一天，公主得知魔王会离开城堡T分钟，这是唯一的一次逃跑机会，但是城堡就像一个三维的迷宫，有些地方不能通行。公主每分钟能从一个坐标走到相邻的六个坐标中的其中一个。现在给你城堡的地图，请你计算出公主能否在魔王回来前离开城堡（只要T分钟刚好走到出口就算离开城堡）。如果可以请输出需要多少分钟才能离开，如果不能则输出-1。

输入要求

输入数据的第一行是一个正整数K，表明测试数据的数量。每组测试数据的第一行是四个正整数A，B，C和T(1<=A,B,C<=50,1<=T<=1000)，它们分别代表城堡的大小和魔王回来的时间。然后是A块输入数据(先是第0块,然后是第1块,第2块…)，每块输入数据有B行，每行有C个正整数，代表三维迷宫的布局。其中0代表路，1代表墙。

输出要求

对于每组测试数据，如果公主能够在魔王回来前离开城堡，那么请输出最少需要多少分钟，否则输出-1。

输入：

1

3 3 4 20

0 1 1 1

0 0 1 1

0 1 1 1

1 1 1 1

1 0 0 1

0 1 1 1

0 0 0 0

0 1 1 0

0 1 1 0

输出：

11

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
#include <bits/stdc++.h>  
using namespace std;  
int a[60][60][60]={0};  
int direction[2] = {1, -1};  
queue<pair<int, pair<int, int>>> q;  
int A, B, C, T;  
int lx, ly, lz;  
//  
int foo(int p, int border, int nextX, int nextY, int nextZ)  
{  
	//如果在范围内并且这个位置没走过，将这个点入栈，并标记已经走过  
	if (p >= 0 && p < border && a[nextX][nextY][nextZ] == 0)  
	{  
		a[nextX][nextY][nextZ] = a[lx][ly][lz] + 1;  
		q.push({nextX, {nextY, nextZ}});  
	}  
}  
int bar(int nextX, int nextY, int nextZ, int i)  
{  
	//每个维度分别从两个方向进行遍历  
	nextX = lx + direction[i];  
	nextY = ly;  
	nextZ = lz;  
	foo(nextX, A, nextX, nextY, nextZ);  
	nextX = lx;  
	nextY = ly + direction[i];  
	nextZ = lz;  
	foo(nextY, B, nextX, nextY, nextZ);  
	nextX = lx;  
	nextY = ly;  
	nextZ = lz + direction[i];  
	foo(nextZ, C, nextX, nextY, nextZ);  
}  
int main()  
{  
	int t;  
	cin >> T;  
	while (T--)  
	{  
		//三维地图输入  
		cin >> A >> B >> C >> t;  
		for (int i = 0; i < A; i++)  
		{  
			for (int j = 0; j < B; j++)  
			{  
				for (int k = 0; k < C; k++)  
				{  
					cin >> a[i][j][k];  
				}  
			}  
		}  
		//起点入队列  
		q.push({0, {0, 0}});  
		//起点标记为1，表示已经走过  
		a[0][0][0] = 1;  
		//只要队列不空，就一直弹出  
		while (!q.empty())  
		{  
			//获得队列首  
			pair<int, pair<int, int>> now = q.front();  
			q.pop();  
			//用来保存当前坐标  
			lx = now.first, ly = now.second.first, lz = now.second.second;  
			int nextX, nextY, nextZ;  
			//三个维度每个维度两个方向进行遍历  
			for (int i = 0; i <2; i++)  
			{  
				bar(nextX, nextY, nextZ, i);  
			}  
		}  
		if (a[A - 1][B - 1][C - 1] - 1 <= t)  
			cout << a[A - 1][B - 1][C - 1] - 1 << endl;  
		else  
			cout << -1 << endl;  
	}  
}


装载问题-优先队列法

来源：https://blog.csdn.net/qq_44766883/article/details/106904355

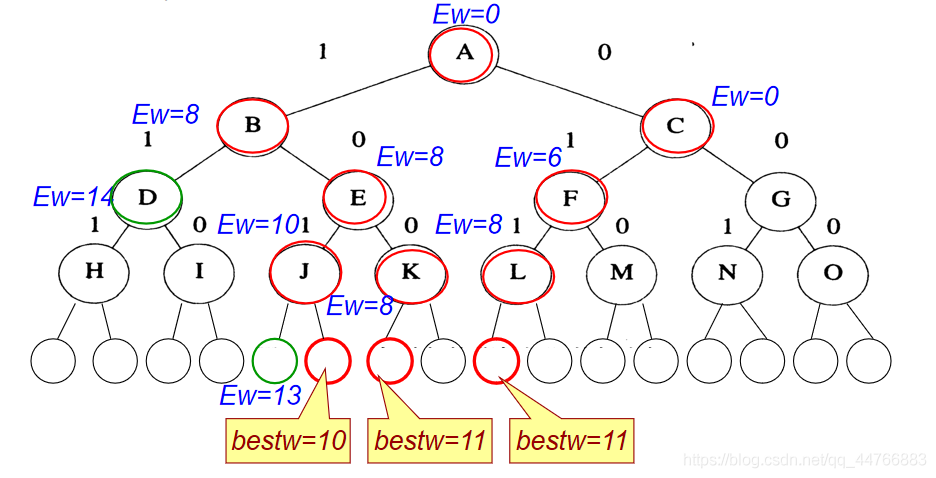
队列式分支限界法

  • 解装载问题的队列式分支限界法仅求出所要求的最优值，稍后进一步构造最优解。
  • 首先检测当前扩展结点的左儿子结点是否为可行结点。如果是，则将其加入到活结点队列Q中。
  • 然后，将其右儿子结点加入到活结点队列中(右儿子结点一定是可行结点)。2个儿子结点都产生后，当前扩展结点被舍弃。
  • 活结点队列中，队首元素被取出作为当前扩展结点。
  • 活结点队列已空，算法终止。

例子

例如 n=4, c1=12, w=[8, 6, 2, 3].

注：

  • 叶子结点不会被扩展，因此不用加入到活结点队列当中，此时，只需要检查该叶节点表示的最优解是否优于当前最优解，并实时更新当前最优解。
  • 同层尾部标记：-1

活结点队列

当取出的元素是-1时，判断当前队列是否为空?

  • 如果队列不空，则将尾部标记 -1加入到活节点队列中，代表算法开始处理下一层活节点，即：代表算法开始处理 下一个物品的装载问题（每一层i开始处理第i个物品的装载）。
  • 如果为空，说明处理完毕，输入bestw并退出

伪代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
#include <bits/stdc++.h>
using namespace std;
typedef struct QNode
{
    QNode *parent;
    int lchild;
    int weight;
}QNode;
int n;
int c;
int bestw;
int w[100];
int bestx[100];
void InPut()
{
    scanf("%d %d", &n, &c);
    for(int i = 1; i <= n; ++i)
        scanf("%d", &w[i]);
//    for(int i = 1; i <= n; ++i)
//        printf("%d ", w[i]);
//    cout << endl;
//    printf("输入结束\n");
}
//QNode *&bestE 的原因是 首先bestE是个地址， 其次引用为了赋值使用, 后边for循环中用到
void EnQueue(queue<QNode *> &q, int wt, int i, QNode *E, QNode *&bestE, int ch)
{
    if(i == n)
    {
        if(wt == bestw)
        {
            bestE = E;
            bestx[n] = ch;
            return;
        }
    }
    QNode *b;
    b = new QNode;
    b->weight = wt;
    b->lchild = ch;
    b->parent = E;
    q.push(b);
}
int MaxLoading()
{
    queue<QNode *>q;
    q.push(0);
    int i = 1;
    //Ew表示已经将
    int Ew = 0, r = 0;
    bestw = 0;
    for(int j = 2; j <= n; ++j)
        r += w[j];
    QNode *E, *bestE; //bestE的作用是：结束while循环后，bestE指向最优解的叶子节点，然后通过bestE->parent找到装入了哪些物品。
    E = new QNode; //E这里作为一个中间量，连接parent和child
    E = 0;         //赋0是因为树的根的值是0，while刚开始的时候其代表root
    while(true)
    {
        int wt = Ew + w[i];
        if(wt <= c)
        {
            if(wt > bestw)   //提前更新bestW,注意更新条件
                bestw = wt;
            EnQueue(q, wt, i, E, bestE, 1);
        }
        if(Ew + r >= bestw)   //右儿子剪枝
        {
            EnQueue(q, Ew, i, E, bestE, 0);    
        }
        E = q.front();
        q.pop();
        if(!E)    //如果取得的数是0，代表该处理下一层
        {
            if(q.empty())   //如果队列为空，表示该循环结束了
                break;
            q.push(0);     //如果队列中还有数据，表示循环还没结束。在该层的末尾加一个0标识符
            E = q.front();
            q.pop();
            i++;     //下一层走起
            r -= w[i];   //计算剩余的重量
        }
        Ew = E->weight; //不要忘记更新最新节点的值
    }
    for(int j = n - 1; j > 0; --j)
    {
        bestx[j] = bestE->lchild;
        bestE = bestE->parent;
    }
}
void OutPut()
{
    printf("最优装载量为 %d\n", bestw);
    printf("装载的物品为 \n");
    for(int i = 1; i <= n; ++i)
        if(bestx[i] == 1)
          printf("%d ", i);
}
int main()
{
    InPut();
    MaxLoading();
    OutPut();
}

填涂格子

题目

有一个由数字 0、1 组成的方阵中，存在一任意形状的封闭区域，封闭区域由数字1 包围构成，每个节点只能走上下左右 4 个方向。现要求把封闭区域内的所有空间都填写成2 .例如： 6×6 的方阵：

输入要求

每组测试数据第一行一个整数 n(1≤n≤30)

接下来 n 行，由 0 和 1 组成的 n×n 的方阵。

封闭区域内至少有一个0 。

输入

6

0 1 0 0 0 0

1 0 1 1 1 1

0 1 1 0 0 1

1 1 0 0 0 1

1 0 0 0 0 1

1 1 1 1 1 1

输出

0 1 0 0 0 0

1 2 1 1 1 1

0 1 1 2 2 1

1 1 2 2 2 1

1 2 2 2 2 1

1 1 1 1 1 1

思路

0 1 0 0 0 0

1 0 1 1 1 1

0 1 1 0 0 1

1 1 0 0 0 1

1 0 0 0 0 1

1 1 1 1 1 1

  • 从地图的外围出发，从上面标红的点出发，进行深度搜索，只要能走通，就将其标记为3（或者其它数字）
  • 输入地图后，需要设置上下、左右边界为1表示墙
  • 判断地图某个点能否走的标准：arr[x][y]==0
  • 最终打印结果时，判断arr[x][y]的值，只要遇到3，说明是可以走通的，说明不是封闭区域，输出0；如果遇到0，说明是封闭区域，输出2；遇到1说明是墙，输出1

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
#include <bits/stdc++.h>
using namespace std;
int a[50][50];
int mark[50][50]= {0};
//设置四个方向
int d[4][4]= {{1,0,-1,0},{0,1,0,-1}};
int n;

void dfs(int x,int y) {
	int nextX,nextY;
    //能走通都标记为3
	a[x][y]=3;
    //从四个方向上进行搜索
	for(int i=0; i<4; i++) {
		nextX=x+d[0][i];
		nextY=y+d[1][i];
        //如果在地图范围内并且未探索
		if(a[nextX][nextY]==0) {
			dfs(nextX,nextY);
		}
	}
	return ;
}
int main() {
	cin>>n;
	for(int i=1; i<=n; i++)
		for(int j=1; j<=n; j++)
			cin>>a[i][j];
	//设置左右边界，让边界点变成-1
    for(int i=0;i<=n+1;i++){
        a[i][0]=a[i][n+1]=-1;
    }
    //设置上下边界，让边界点变成-1
    for(int i=0;i<=n+1;i++){
        a[0][i]=a[n+1][i]=-1;
    }
	for(int i=1; i<=n; i++) {
		//从地图外围开始向内走，如果能走通，说明这个地区没被围，将mark置为1
		if(a[1][i]==0) dfs(1,i);
		if(a[n][i]==0) dfs(n,i);
		if(a[i][1]==0) dfs(i,1);
		if(a[i][n]==0) dfs(i,n);
	}
	cout<<endl;
    //打印结果
	for(int i=1; i<=n; i++) {
		for(int j=1; j<=n; j++) {
			cout<<a[i][j]<<" ";
		}
		cout<<endl;
	}
	cout<<endl;
	for(int i=1; i<=n; i++) {
		for(int j=1; j<=n; j++) {
            //将位置标志为0而且值为0输出为2，表示填充为封闭区域
			if(a[i][j]==0) {
				cout<<"2 ";
			} else if(a[i][j]==3){
				cout<<"0 ";
			}else{
				cout<<a[i][j]<<" ";
			}
		}
		cout<<endl;
	}
}

填涂最大格子

题目

有一个由数字 0、1 组成的方阵中，存在一任意形状的封闭区域，封闭区域由数字1 包围构成，每个节点只能走上下左右 4 个方向。现要求只把**【最大封闭区域】**内的空间填写成2 。

输入要求

每组测试数据第一行一个整数 n(1≤n≤30)

封闭区域内至少有一个0，测试数据保证最大区域只有一个。

输入

例如： 6×6 的方阵：

6

0 1 0 0 0 0

1 0 1 1 1 1

0 1 1 0 0 1

1 1 0 0 0 1

1 0 0 0 0 1

1 1 1 1 1 1

输出

0 1 0 0 0 0

1 0 1 1 1 1

0 1 1 2 2 1

1 1 2 2 2 1

1 2 2 2 2 1

1 1 1 1 1 1

思路

和填涂格子思路不同，因为需要找最大格子，所以需要进入到封闭区间内。

  • 需要以地图内所有位置为起点开始，进行深度搜索
  • 每次搜索时，使用一个染色id，同一批的搜索使用同一个id（填涂格子时，将arr[i][j]标记为3），这次将arr[i][j]标记id【会出现从后一个起点出发的，覆盖掉从之前出发并已经染色的点】
  • 以某个位置为起点的搜索结束后，判断，这次搜索到的格子数是否大于记录到的最大值。如果是，则修正最大值，并记录对应的染色id为最大染色区id。 （无论是否）将id+1，并继续以下一个位置为起点进行搜索
  • 输出时，需要将arr[i][j]等于最大染色区id输出为2即可(说明对应染色id的格子数最多，不代表id数本身是最大的)

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
#include<iostream>
#include<cstring>
using namespace std;

int a[35][35] = {0}; 
int n;
//四个方向
int dir[4][2] = {{1, 0}, {-1, 0}, {0, 1}, {0, -1}};
int cnt = 0; //某个封闭区域大小
int cnt_max = 0; //最大封闭区域大小
int id = 3; //染色区域的编号，从3开始，当然可以从其它的开始，大于2即可
int id_max = id;

void prit()
{
	int i,j;
	for( i = 1; i <= n; i++) {
	for( j = 1; j <= n; j++) {
		if(a[i][j] == 1) {
			cout << a[i][j] << ' ';
		} 
		else if(a[i][j] != id_max){
			cout << '0' << ' ';
		}
        //如果封闭区域为最大封闭区域的号，才输出
		else {
			cout << '2' << ' ';
		}
	}
	cout << endl;
}	
} 

void dfs(int x, int y)//将与其邻接的0坐标改为id
{
	int nextX,nextY;
    // 将当前位置染色为[应该染色成的]id【上面填涂格子不同，上面设置为任意值，这里设置为id】
	a[x][y] = id;
    //被染色的块数加1
	cnt++;
    //从四个方向进行深度搜索 
	for(int i = 0; i < 4; i++) {
		nextX=x+dir[i][0];
		nextY=y+dir[i][1];
        //如果在地图范围内并且未探索
		if(a[nextX][nextY]==0) {
			dfs(nextX,nextY);
		}
	}
	return ; 
}

int main() {
	int i,j;
	cin >> n;
	for( i = 1; i <= n; i++){
		for( j = 1; j <= n; j++) {
			cin >> a[i][j];
		}
	}
	//设置左右边界，让边界点变成1
    for(int i=0;i<=n+1;i++){
        a[i][0]=a[i][n+1]=1;
    }
    //设置上下边界，让边界点变成1
    for(int i=0;i<=n+1;i++){
        a[0][i]=a[n+1][i]=1;
    }
	
    //最外围的0不形成封闭区域
	// dfs(0, 0);
    //从第二层开始形成封闭区域【因为要向第一层搜索
	for( i = 2; i < n; i++) {
		for( j = 2; j < n; j++) {
			//如果这个位置为起点未被搜索
			if(a[i][j]==0)
				dfs(i, j);
            //如果有封闭区域的块数大于记录的最大封闭区域块数，则修正
			if(cnt > cnt_max){
				cnt_max = cnt;
				//记录下对应id
				id_max = id;
			}
            //每次染色完成后，下一个染色区域id加1
			id++;	
            //每次用来记录某个区间的计数器设置为0
			cnt = 0;
		}
	}
	//输出运算后的原始map
	cout<<endl;
	for(int i=1; i<=n; i++) {
		for(int j=1; j<=n; j++) {
			printf("%3d",a[i][j]);
		}
		cout<<endl;
	}
	cout<<endl;

	//打印结果
	prit();
	return 0;
}