LeetCodeCampsDay14-二叉树part02

继续使用深度/广度遍历解决问题，包含迭代&递归的方法

翻转二叉树

https://leetcode.cn/problems/invert-binary-tree/

给你一棵二叉树的根节点 root ，翻转这棵二叉树，并返回其根节点。

示例 1：

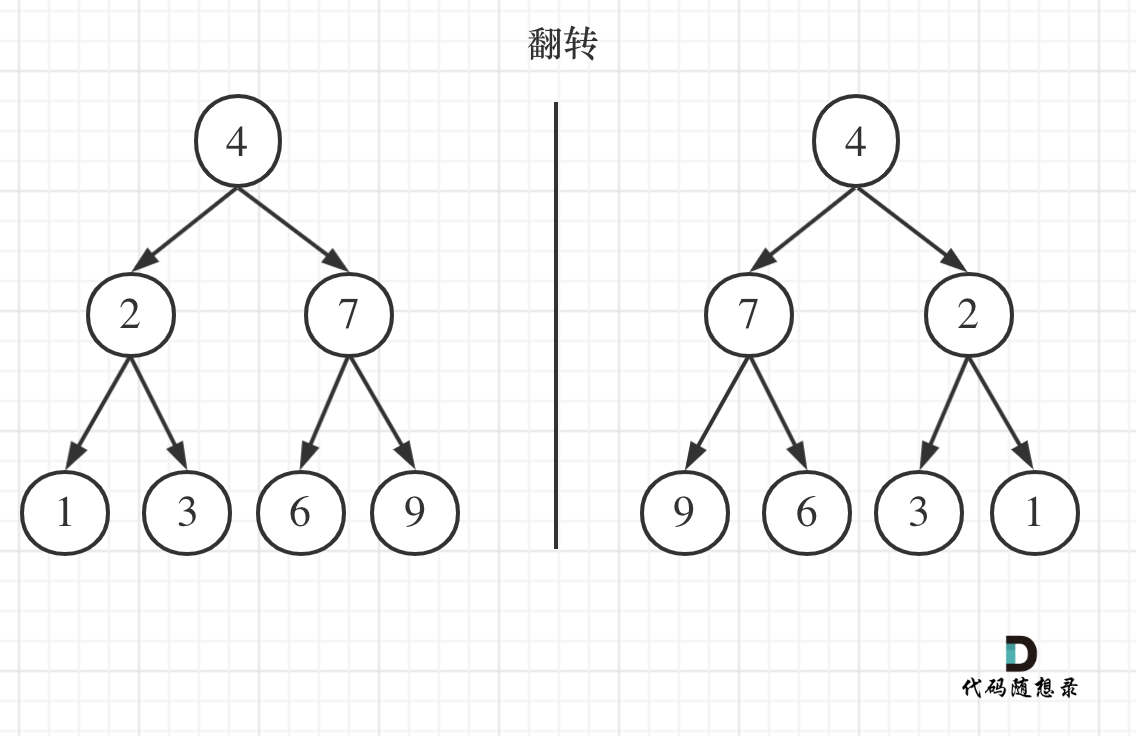
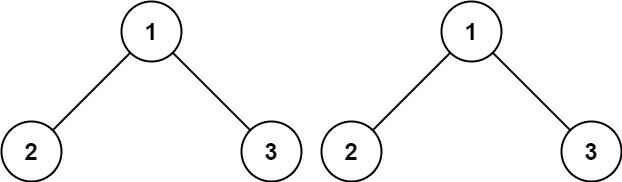
输入：root = [4,2,7,1,3,6,9]
输出：[4,7,2,9,6,3,1]

示例 2：

输入：root = [2,1,3]
输出：[2,3,1]

示例 3：

输入：root = []
输出：[]

提示：

• 树中节点数目范围在 [0, 100] 内
• -100 <= Node.val <= 100

递归思路

可以发现想要翻转它，其实就把每一个节点的左右孩子交换一下就可以了。

1. 可以按“前序/中序/后序”的方法，将中间节点进行“调换”，然后用递归的方式去处理左、右子树
2. 递归三步走：返回值与输入值；终止条件（传入node为空）；单层递归的逻辑（调换node的左右子树，再执行递归处理左、右子树）

递归代码

前序递归

• 时间复杂度O(N)
• 空间复杂度O(h)，其中，h为树的高度，最坏情况下递归栈的空间用调用O(N)；而最好情况下，即平衡二叉树O(logN)

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def traverse(self, node: TreeNode):
        if not node:
            return
        # 中, 交换两个节点
        node.left, node.right = node.right, node.left
        self.traverse(node.left) #左
        self.traverse(node.right)#右

    def invertTree(self, root: Optional[TreeNode]) -> Optional[TreeNode]:
        self.traverse(root)
        return root

中序递归

这道题目使用前序遍历和后序遍历都可以，唯独中序遍历不方便，因为中序遍历会把某些节点的左右孩子翻转了两次！建议拿纸画一画，就理解了

这题目如果使用中序遍历，需要修改逻辑

class Solution:
    def traverse(self, node: TreeNode):
        if not node:
            return
        
        self.traverse(node.left)  #原左子树
        # 中, 交换两个节点
        node.left, node.right = node.right, node.left
        self.traverse(node.left)  #原右子树，因为刚刚发生了左右翻转，原来的右子树现在是left

    def invertTree(self, root: Optional[TreeNode]) -> Optional[TreeNode]:
        self.traverse(root)
        return root

后序递归

后序递归不用进行特殊处理

class Solution:
    def traverse(self, node: TreeNode):
        if not node:
            return
        
        self.traverse(node.left) #左
        self.traverse(node.right)#右
        # 中, 交换两个节点
        node.left, node.right = node.right, node.left

    def invertTree(self, root: Optional[TreeNode]) -> Optional[TreeNode]:
        self.traverse(root)
        return root

当然，还可以使用栈的方式做这题目（栈+迭代，可以达到递归的效果）

迭代代码(标记法)

• 时间复杂度O(N)
• 空间复杂度O(h)–和递归一样，最坏情况为O(N)，最好情况为O(logN)

def invertTree(self, root: Optional[TreeNode]) -> Optional[TreeNode]:
    stack = [(root, False)] if root else []
    
    while stack:
        node, visit_status = stack.pop()
        if visit_status:
            node.left, node.right = node.right, node.left
        else:
            stack.append((node, True))
            if node.left:
                stack.append((node.left, False))
            if node.right:
                stack.append((node.right, False))
    return root

当然，也可以使用普通的迭代方法，下面是前序迭代遍历

def invertTree(self, root: Optional[TreeNode]) -> Optional[TreeNode]:
    stack = list()
    stack.append(root)
    if not root:
        return root
    
    while stack:
        node = stack.pop()
        # 将结果记录到res的步骤替换成节点交换即可
        node.left, node.right = node.right, node.left
        if node.left:
            stack.append(node.left)
        if node.right:
            stack.append(node.right)
    return root

对称二叉树

https://leetcode.cn/problems/symmetric-tree/

给你一个二叉树的根节点 root ， 检查它是否轴对称。

示例 1：

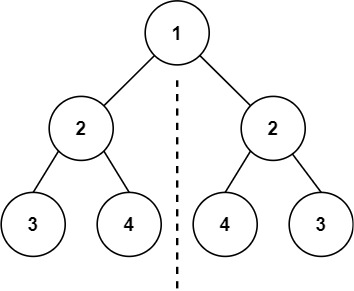
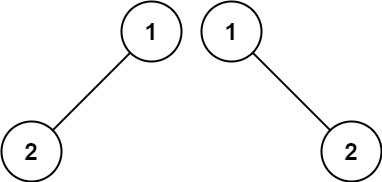
输入：root = [1,2,2,3,4,4,3]
输出：true

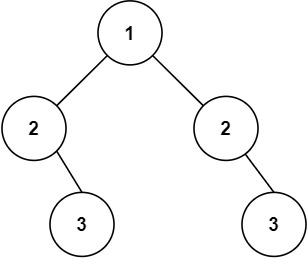
示例 2：

输入：root = [1,2,2,null,3,null,3]
输出：false

提示：

• 树中节点数目在范围 [1, 1000] 内
• -100 <= Node.val <= 100

**进阶：**你可以运用递归和迭代两种方法解决这个问题吗？

思路

1. 如果使用递归的方法解决，仍然需要解决三个问题
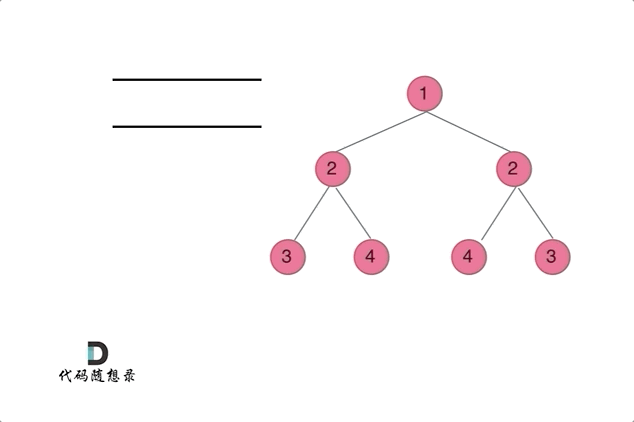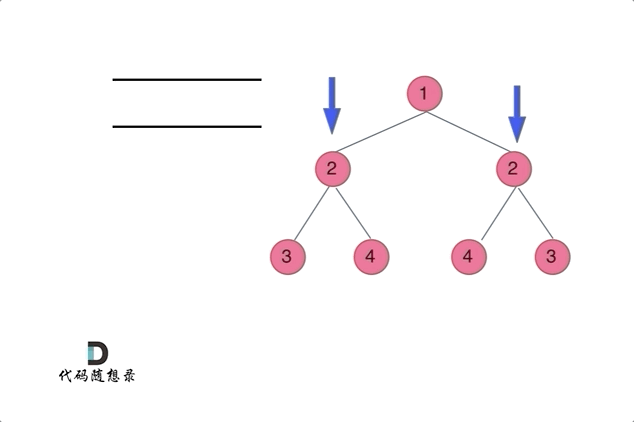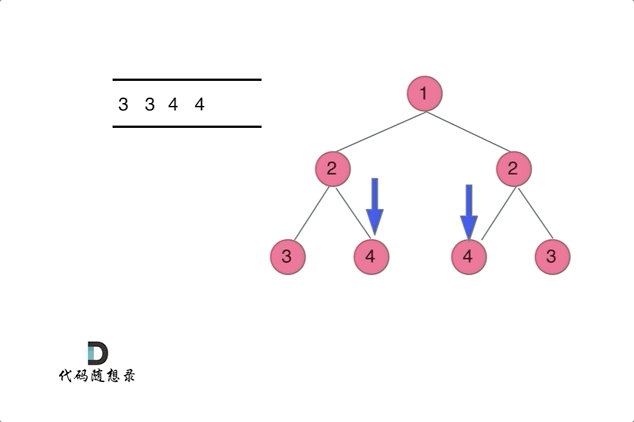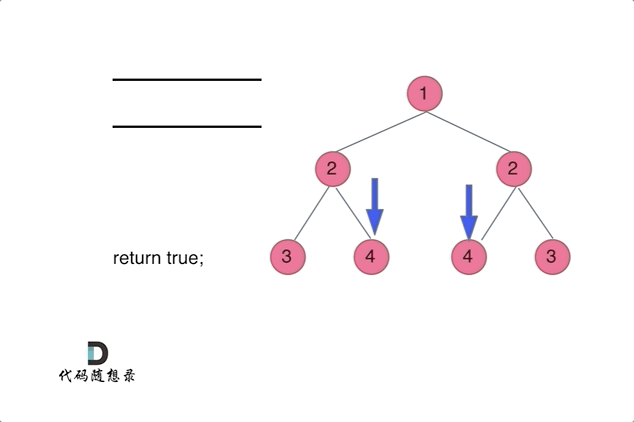
   1. 输入与输出；因为需要判断二叉树是否对称，每次需要判断“左、右”两个节点是否相等，所以输入是leftNode, rightNode
   2. 终止条件：如果leftNode和rightNode都为空，也算是True；leftNode不空而rightNode为空，算False；leftNode为空而rightNode不空，算False；若leftNode和rightNode都不空，但数值不相同，也算False；只有当leftNode和rightNode数值相等时，才进行它俩的子树判断
   3. 单层递归的操作逻辑：先判断终止条件；当leftNode和rightNode数值相等时，才进行它俩的子树判断，这里要判断
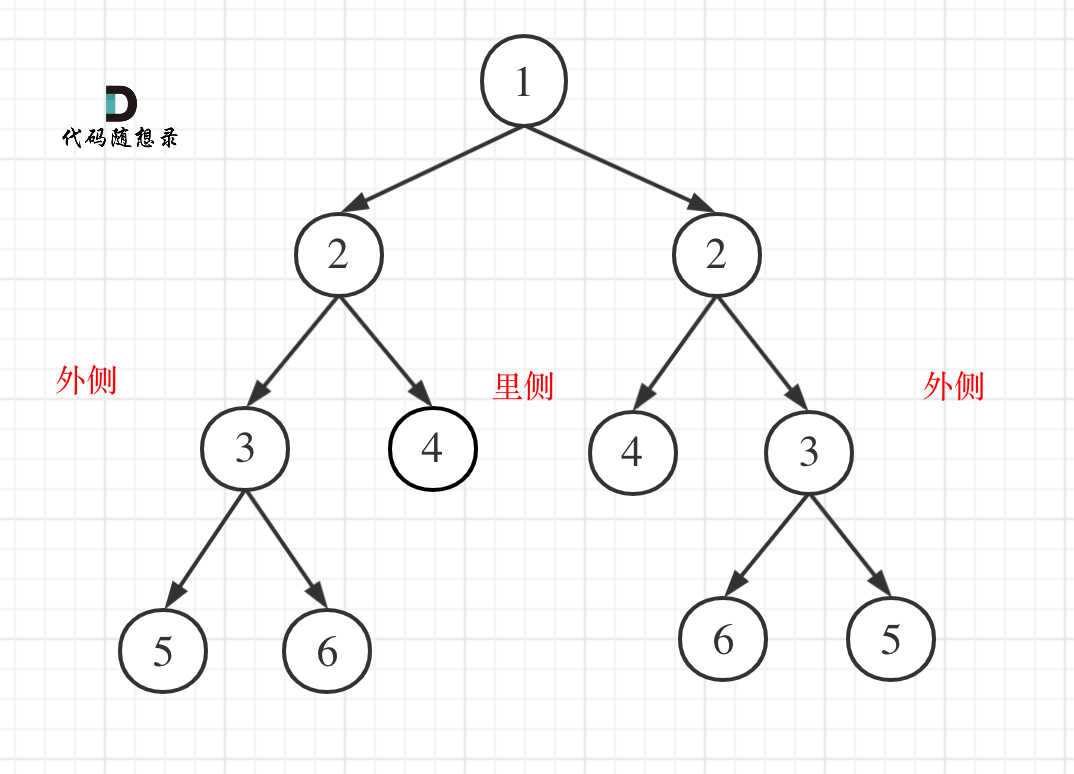
      1. leftNode的左子树与rightNode的右子树是否相等（外部判断）
      2. leftNode的右子树与rightNode的左子树是否相等（内部判断）
      3. 只有内、外都相等时才返回True

代码

• 时间复杂度O(N)
• 空间复杂度O(h)—同样，因为递归调用的空间取决于树的深度，最差情况是O(N)，最好情况是O(logN)

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def traverse(self, leftNode: TreeNode, rightNode: TreeNode) -> bool:
        if leftNode is None and rightNode is not None:
            return False
        elif leftNode is not None and rightNode is None:
            return False
        elif leftNode is None and rightNode is None:
            return True
        elif leftNode.val != rightNode.val:  # 如果都不为空，此时需要判断数值是否相等
            return False
        else:
            # 都不为空，而且数值相等
            outSide = self.traverse(leftNode.left, rightNode.right)
            inSide = self.traverse(leftNode.right, rightNode.left)
            res = outSide and inSide # 仅当内部与外部同时相等时，二叉树才是对称的
            return res

    def isSymmetric(self, root: Optional[TreeNode]) -> bool:
        if not root:
            return False
        return self.traverse(root.left, root.right)

迭代思路

1. 使用队列或栈，每次从栈/队列中取出两个节点，判断它们是否（值一样或都为空），然后再判断他俩的内、外子树是否一致

栈+迭代代码

• 时间复杂度O(N)
• 空间复杂度O(h)—同样，因为栈占用的空间取决于树的深度，最差情况是O(N)，最好情况是O(logN)

def isSymmetric(self, root: Optional[TreeNode]) -> bool:
    stack = list()
    if not root:
        return False
    stack.append(root.left)
    stack.append(root.right)
    while stack:
        # 这里将pop出来的顺序先给rightNode或先出leftNode都可以，效果一样，因为后面的代码是对称的
        rightNode = stack.pop()
        leftNode = stack.pop()
        if not leftNode and not rightNode:
            continue
        if not leftNode or not rightNode or leftNode.val != rightNode.val:
            return False
        # 仅当两个节点值相等时，再判断它的内、外
        
        # 进行外部判断
        stack.append(leftNode.left)
        stack.append(rightNode.right)
        # 进行内部判断
        stack.append(leftNode.right)
        stack.append(rightNode.left)

    return True

队列+迭代代码

把栈（list)换成队列即可

• 时间复杂度O(N)
• 空间复杂度O(h)—同样，因为队列占用的空间取决于树的深度，最差情况是O(N)，最好情况是O(logN)

# 使用队列
from collections import deque
que = deque()
if not root:
    return False
que.append(root.left)
que.append(root.right)

while que:
    # 弹出两个节点
    leftNode = que.popleft()
    rightNode = que.popleft()
    # 判断是否相等（同样为空也是可以的）
    if not leftNode and not rightNode:
        continue
    # 如果不相等直接返回False
    if not leftNode or not rightNode or leftNode.val != rightNode.val:
        return False
    
    # 如果值相等，再判断它俩的内、外子树
    que.append(leftNode.left)
    que.append(rightNode.right)

    que.append(leftNode.right)
    que.append(rightNode.left)
# 如果都没问题，才返回True
return True

层序思路

1. 使用一个队列deque遍历每个节点
2. 每层再使用一个list，将每层的节点都装进来，并且每层结束后进行清算，如果这层不是对称的，则直接返回False

层序遍历代码

• 时间复杂度O(N)
• 空间复杂度O(h)

if not root:
    return False

from collections import deque
que = deque()
que.append(root.left)
que.append(root.right)

while que:
    levelSize = len(que)
    if levelSize % 2 != 0:
        return False
    
    levelRes = list()
    for i in range(levelSize):
        node = que.popleft()
        if node:
            levelRes.append(node.val)
            que.append(node.left)
            que.append(node.right)
        else:
            levelRes.append(None)
    
    # 对每层进行清算，如果levelRes不是一个对称列表，则返回False
    if levelRes != levelRes[::-1]:
        return False

return True

相同的树

https://leetcode.cn/problems/same-tree/

给你两棵二叉树的根节点 p 和 q ，编写一个函数来检验这两棵树是否相同。

如果两个树在结构上相同，并且节点具有相同的值，则认为它们是相同的。

示例 1：

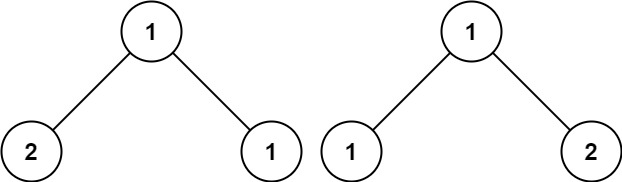
输入：p = [1,2,3], q = [1,2,3]
输出：true

示例 2：

输入：p = [1,2], q = [1,null,2]
输出：false

示例 3：

输入：p = [1,2,1], q = [1,1,2]
输出：false

提示：

• 两棵树上的节点数目都在范围 [0, 100] 内
• -104 <= Node.val <= 104

递归思路

1. 和对称二叉树几乎一样，先取两个节点，判断两个节点值是否一样（如果都为空直接就True）
2. 如果两个节点值一样，再判断他俩的子树，leftNode.left是否等于rightNode.left；并且leftNode.right是否等于rightNode.right；这里和对称二叉树是不一样的，对称二叉树需要判断“内部是否相等，外部是否相等”

递归代码

• 时间复杂度O(N)
• 空间复杂度O(h)—取决于深度；最坏O(N),最好O(logN)

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def traverse(self, leftNode: TreeNode, rightNode: TreeNode) -> bool:
        if not leftNode and not rightNode:
            return True
        elif not leftNode and rightNode:
            return False
        elif leftNode and not rightNode:
            return False
        elif leftNode.val != rightNode.val:
            return False
        else:
            # 当前两个节点值相同，需要判断它俩的内、外子树是否相等（这里和对称不一样）
            outSide = self.traverse(leftNode.left, rightNode.left)
            inSide = self.traverse(leftNode.right, rightNode.right)
            return outSide and inSide

    def isSameTree(self, p: Optional[TreeNode], q: Optional[TreeNode]) -> bool:
        return self.traverse(p, q)

栈+迭代代码

大体思路和递归差不多；主要是终止条件判断，单层逻辑（判断左边是否一样，判断右边是否一样）；两种方法的代码结构几乎一样

• 时间复杂度O(N)
• 空间复杂度O(h)—取决于深度；最坏O(N),最好O(logN)

def isSameTree(self, p: Optional[TreeNode], q: Optional[TreeNode]) -> bool:
    # return self.traverse(p, q)

    stack = list()
    stack.append(p)
    stack.append(q)
    while stack:
        rightNode = stack.pop()
        leftNode = stack.pop()

        if not leftNode and not rightNode:
            continue
        elif not leftNode and rightNode:
            return False
        elif leftNode and not rightNode:
            return False
        elif leftNode.val != rightNode.val:
            return False
        else:
            # 判断左边是否一样
            stack.append(leftNode.left)
            stack.append(rightNode.left)

            # 判断右边是否一样
            stack.append(leftNode.right)
            stack.append(rightNode.right)
    
    return True

另一棵树的子树

https://leetcode.cn/problems/subtree-of-another-tree/

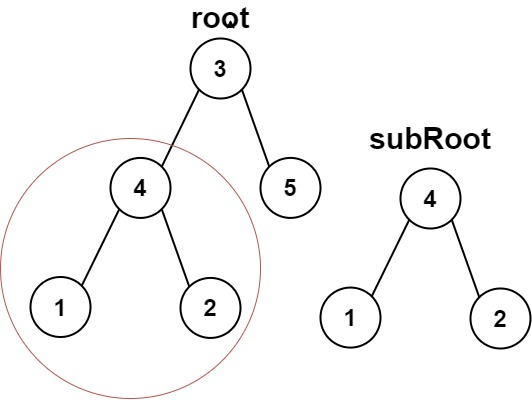
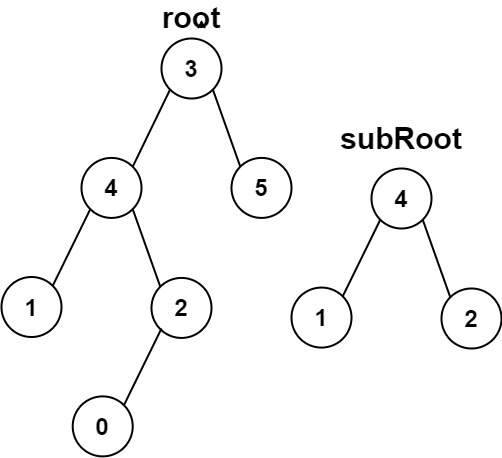
给你两棵二叉树 root 和 subRoot 。检验 root 中是否包含和 subRoot 具有相同结构和节点值的子树。如果存在，返回 true ；否则，返回 false 。

二叉树 tree 的一棵子树包括 tree 的某个节点和这个节点的所有后代节点。tree 也可以看做它自身的一棵子树。

示例 1：

输入：root = [3,4,5,1,2], subRoot = [4,1,2]
输出：true

示例 2：

输入：root = [3,4,5,1,2,null,null,null,null,0], subRoot = [4,1,2]
输出：false

提示：

• root 树上的节点数量范围是 [1, 2000]
• subRoot 树上的节点数量范围是 [1, 1000]
• -104 <= root.val <= 104
• -104 <= subRoot.val <= 104

暴力思路

1. 使用前/中/后序进行遍历，并且对每个节点进行匹配

暴力代码

• 时间复杂度O(N*M)，N为root节点数，M为subRoot节点数
• 空间复杂度O(H)，然后取决于root树的高度

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def isSame(self, leftNode, rightNode) -> bool:
        if not leftNode and not rightNode:
            return True
        elif not leftNode or not rightNode or leftNode.val != rightNode.val:
            return False
        else:
            leftSideSame = self.isSame(leftNode.left, rightNode.left)
            rightSideSame = self.isSame(leftNode.right, rightNode.right)
            return leftSideSame and rightSideSame

    def isSubtree(self, root: Optional[TreeNode], subRoot: Optional[TreeNode]) -> bool:
        # 明确了只可能root包含subRoot，其中判断子树是否一样和100.相同的树同样的思路
        # 最暴力的写法是每个root节点都检测一遍
        # 前序遍历(标记法)
        stack = [(root, False)] if root else []
        res = False
        while stack:
            node, visited = stack.pop()
            if visited:
                res = self.isSame(node, subRoot)
                if res:
                    print(node)
                    return True
            else:
                # 前序
                stack.append((node, True))
                if node.left:
                    stack.append((node.left, False))
                if node.right:
                    stack.append((node.right, False))
        return False
           

KMP匹配思路

1. 如果先使用前/中/后序将root与subRoot遍历一遍，得到的不就是两串字符串序列，然后就可以使用KMP匹配方法解决
2. 但，这里有个需要注意的点，不能使用常规的前/中/后序遍历，而是需要使用下面这种方式：引入两个空值 lNull 和 rNull，当一个节点的左孩子或者右孩子为空的时候，就插入这两个空值，这样深度优先搜索序列就唯一对应一棵树
   1. 比如[4,1,2]得到的前序遍历是[4,1,lNone,rNone,2,lNone,rNone]
   2. 而[4,1]得到的前序遍历是[4,1,lNone,rNone,rNone]
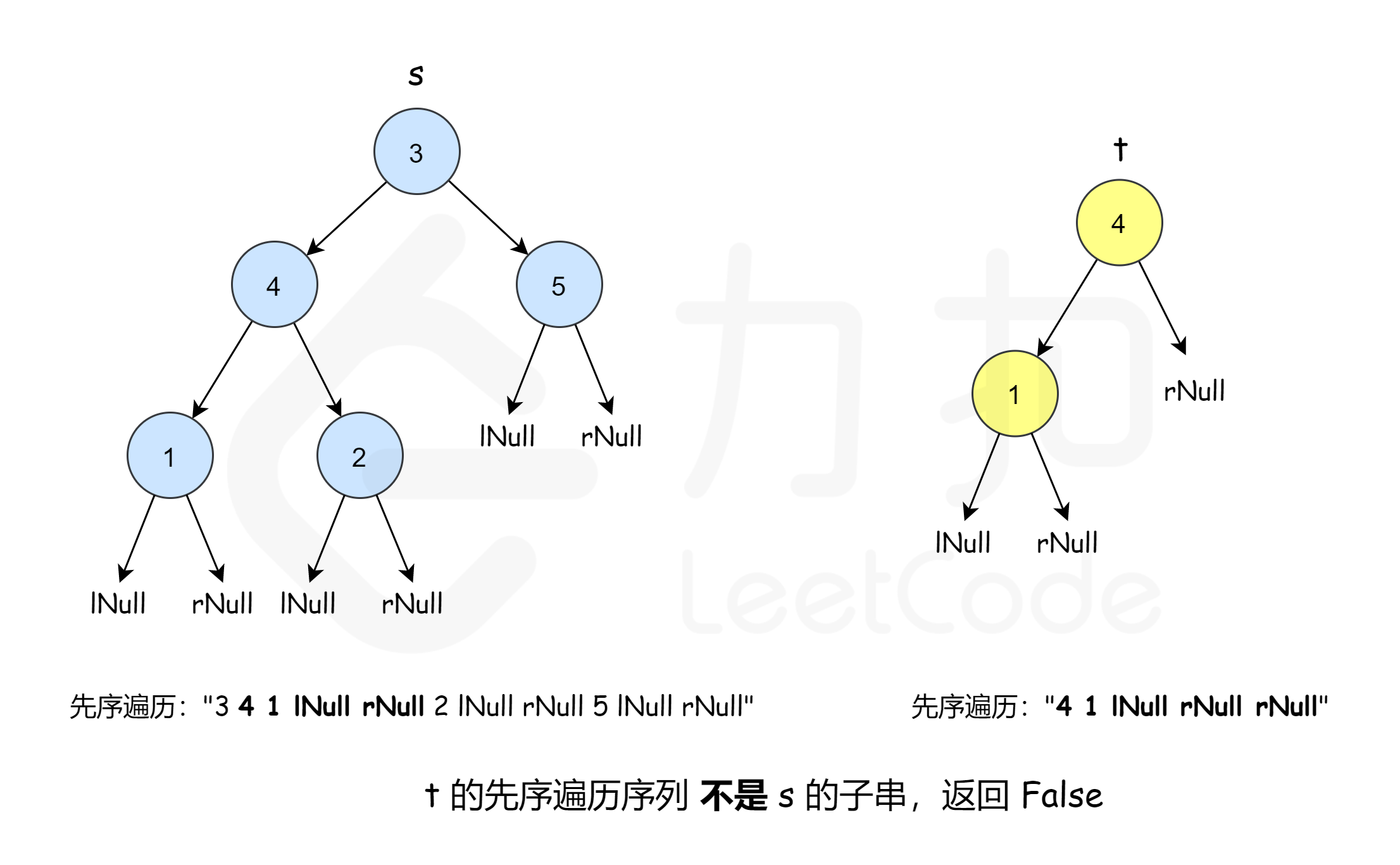
3. 如果不这样做，会遇到一类错误，比如root是[3,4,5,1,2,null,null,null,null,0]；而subRoot是[4,1,2]
4. 
   1. 使用普通前序遍历后，得到[3, 4, 1, 2, 0, 5]和[4,1,2]，如果直接使用KMP进行匹配，会得到True的错误结果；
   2. 使用修改后的前序遍历，得到[3, 4, ‘r’, ‘l’, 1, ‘r’, 2, ‘r’, ‘l’, 0, ‘r’, ‘l’, 5] 和 [4, ‘r’, ‘l’, 1, ‘r’, ‘l’, 2]，此时再用KMP匹配就正确了

KMP代码

• 时间复杂度O(N+M)
• 空间复杂度O(N)

class Solution:
    # 需要对这个前序遍历进行修改，引入lNone与rNone两个值，当一个节点的左/右节点为空，就赋值这个空值
    # 这样好处是产生“唯一”的对应树
    def preOrder(self, root) -> list:
        stack = [(root, False)] if root else []
        res = list()
        while stack:
            node, visited = stack.pop()
            if visited:
                res.append(node.val)
                # 在这里修改，当一个节点的左/右节点为空，就赋值这个空值
                if not node.left:
                    res.append("l")
                if not node.right:
                    res.append('r')
            else:
                # 前序
                stack.append((node, True))
                if node.left:
                    stack.append((node.left, False))
                if node.right:
                    stack.append((node.right, False))
        # 需要反转
        res = res[::-1]
        return res

    def getNext(self, s: list) -> list:
        L = len(s)
        nextArray = [0] * L
        left = 0
        for right in range(1, L):
            while left > 0 and s[left] != s[right]:
                left = nextArray[left - 1]
            if s[left] == s[right]:
                left = left + 1
            nextArray[right] = left
        return nextArray

    def isSubtree(self, root: Optional[TreeNode], subRoot: Optional[TreeNode]) -> bool:
        rootList = self.preOrder(root)
        subRootList = self.preOrder(subRoot)
        nextArray = self.getNext(subRootList)
        # print(rootList)
        # print(subRootList)
        left = 0
        L_subRoot = len(subRootList)
        L_root = len(rootList)
        for right in range(L_root):
            while left > 0 and rootList[right] != subRootList[left]:
                left = nextArray[left - 1]
            if rootList[right] == subRootList[left]:
                left = left + 1
            if left == L_subRoot:
                return True
        return False

或者使用递归版本的前序遍历

def preOrderTraverse(self, node, res):
    if not node:
        return
    res.append(node.val)
    if node.left:
        self.preOrderTraverse(node.left, res)
    else:
        res.append('l')
    if node.right:
        self.preOrderTraverse(node.right, res)
    else:
        res.append('r')

二叉树的最大深度

https://leetcode.cn/problems/maximum-depth-of-binary-tree/

给定一个二叉树 root ，返回其最大深度。

二叉树的 最大深度 是指从根节点到最远叶子节点的最长路径上的节点数。

示例 1：

输入：root = [3,9,20,null,null,15,7]
输出：3

示例 2：

输入：root = [1,null,2]
输出：2

提示：

• 树中节点的数量在 [0, 104] 区间内。
• -100 <= Node.val <= 100

后序递归思路

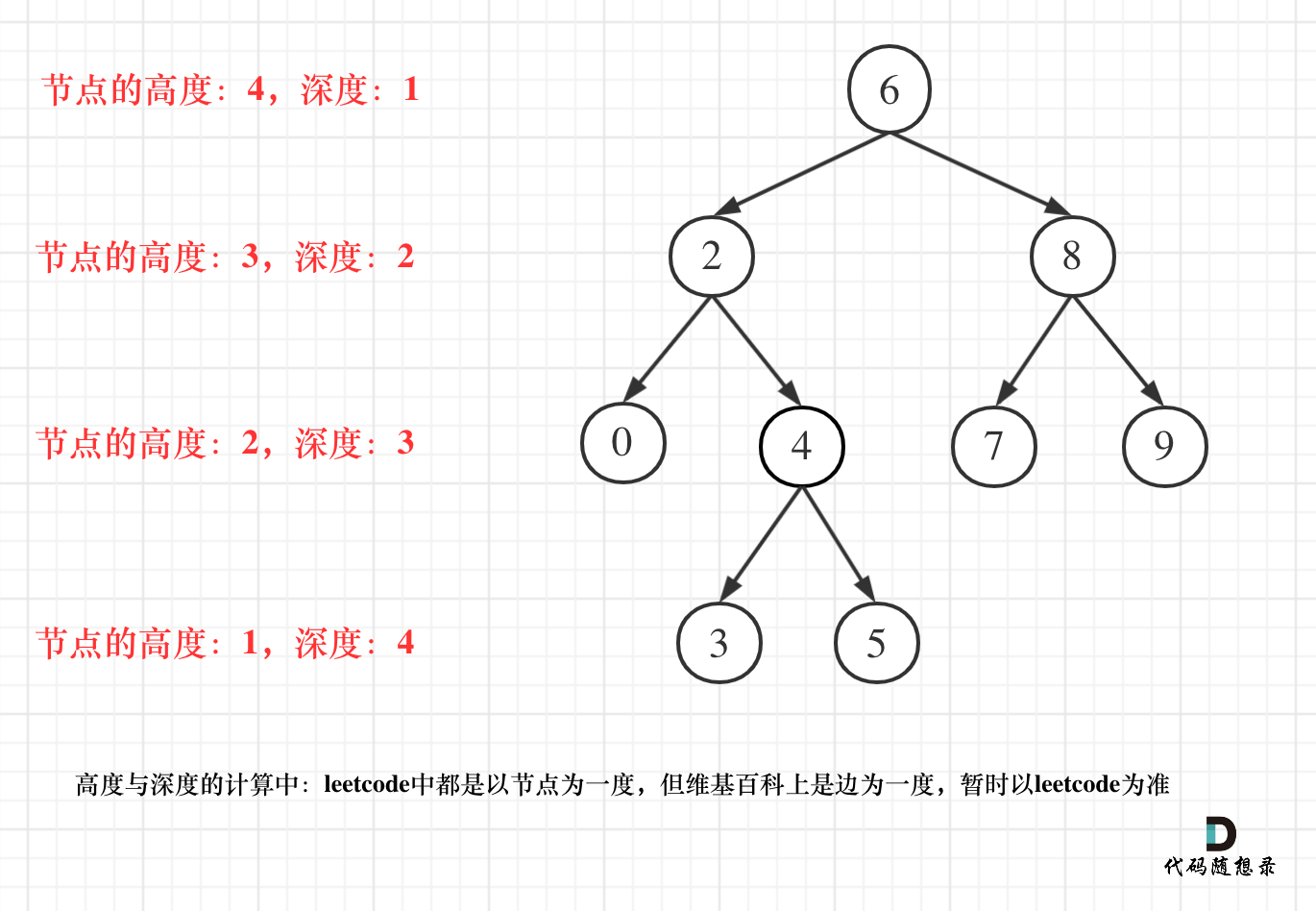
补充下什么是深度与高度，这里要求“最大深度”，其实就是求“根节点的高度”

1. 根节点的高度就是二叉树的最大深度，所以本题中我们通过后序求的根节点高度来求的二叉树最大深度
2. 确定递归函数的参数和返回值：参数就是传入树的根节点，返回就返回这棵树的深度，所以返回值为int类型
3. 确定终止条件：如果为空节点的话，就返回0，表示高度为0
4. 确定单层递归的逻辑：先求它的左子树的深度，再求右子树的深度，最后取左右深度最大的数值 再+1 （加1是因为算上当前中间节点）就是目前节点为根节点的树的深度。

所以这里的代码也同样是求高度的代码，还是比较好写的

如果要求某个节点所在位置的深度，有个思路是，根节点到这个节点的路径是唯一的，可以求出这路径长度，即是深度；至于怎么求这个路径，可以参考day15的「二叉树的所有路径」

后序递归代码

• 时间复杂度O(N)
• 空间复杂度O(h) 最坏情况O(N)

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def traverse(self, node) -> int:
        if not node:
            return 0
        
        leftDeepth = self.traverse(node.left)
        rightDeepth = self.traverse(node.right)
        return max(leftDeepth, rightDeepth) + 1
        
    def maxDepth(self, root: Optional[TreeNode]) -> int:
        return self.traverse(root)

迭代思路

1. 层序遍历就是最好求深度的过程

迭代代码

• 时间复杂度O(N)
• 空间复杂度O(N)

def maxDepth(self, root: Optional[TreeNode]) -> int:
    from collections import deque
    if not root:
        return 0
    que = deque()
    que.append(root)
    level = 0
    while que:
        L = len(que)
        for i in range(L):
            node = que.popleft()
            if node.left:
                que.append(node.left)
            if node.right:
                que.append(node.right)
        # 每层的操作（结算）
        level += 1
    return level

N 叉树的最大深度

https://leetcode.cn/problems/maximum-depth-of-n-ary-tree/

给定一个 N 叉树，找到其最大深度。

最大深度是指从根节点到最远叶子节点的最长路径上的节点总数。

N 叉树输入按层序遍历序列化表示，每组子节点由空值分隔（请参见示例）。

示例 1：

输入：root = [1,null,3,2,4,null,5,6]
输出：3

示例 2：

输入：root = [1,null,2,3,4,5,null,null,6,7,null,8,null,9,10,null,null,11,null,12,null,13,null,null,14]
输出：5

提示：

• 树的深度不会超过 1000 。
• 树的节点数目位于 [0, 104] 之间。

迭代思路

1. 使用层序遍历，和二叉树的层序遍历求最大深度基本一样

迭代代码

• 时间复杂度O(N)
• 空间复杂度O(N) which can scale with the tree’s width. 最多是树的宽度

"""
# Definition for a Node.
class Node:
    def __init__(self, val: Optional[int] = None, children: Optional[List['Node']] = None):
        self.val = val
        self.children = children
"""

class Solution:
    def maxDepth(self, root: 'Node') -> int:
        # 注意n叉树的子节点是个列表
        # 本题可以使用层序遍历
        from collections import deque
        if not root:
            return 0
        que = deque()
        que.append(root)
        levels = 0
        while que:
            L = len(que)
            for i in range(L):
                node = que.popleft()
                for eachNode in node.children:
                    que.append(eachNode)
            levels += 1
        return levels

递归代码

def traverse(self, node) -> int:
    if not node:
        return 0
    deepthList = []
    for eachNode in node.children:
        deepthList.append(self.traverse(eachNode))
    # 除了这层本身还有它的子树，加max of 子树
    if len(deepthList):
        return 1 + max(deepthList)
    # 这层本身
    else:
        return 1

二叉树的最小深度

https://leetcode.cn/problems/minimum-depth-of-binary-tree/

给定一个二叉树，找出其最小深度。

最小深度是从根节点到最近叶子节点的最短路径上的节点数量。

**说明：**叶子节点是指没有子节点的节点。

示例 1：

输入：root = [3,9,20,null,null,15,7]
输出：2

示例 2：

输入：root = [2,null,3,null,4,null,5,null,6]
输出：5

提示：

• 树中节点数的范围在 [0, 105] 内
• -1000 <= Node.val <= 1000

递归后序思路

求最大深度时，使用了下面的代码

int leftDepth = getDepth(node->left);
int rightDepth = getDepth(node->right);
int result = 1 + min(leftDepth, rightDepth);
return result;

如果这么求的话，没有左孩子的分支会算为最短深度。

所以，如果左子树为空，右子树不为空，说明最小深度是 1 + 右子树的深度。

反之，右子树为空，左子树不为空，最小深度是 1 + 左子树的深度。

最后如果左右子树都不为空，返回左右子树深度最小值 + 1 。

求二叉树的最小深度和求二叉树的最大深度的差别主要在于处理左右孩子不为空的逻辑。

递归后序代码

• 时间复杂度O(N)
• 空间复杂度O(H)

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def traverse(self, node):
        if not node:
            return 0
        leftDeepth = self.traverse(node.left)
        rightDeepth = self.traverse(node.right)
        # 如果左节点为空，则求右节点的deepth+1
        if not node.left and node.right:
            return 1 + rightDeepth
        if not node.right and node.left:
            return 1 + leftDeepth
        # 
        return min(leftDeepth, rightDeepth) + 1

    def minDepth(self, root: Optional[TreeNode]) -> int:
        return self.traverse(root)

迭代思路

1. 使用层序遍历即可，但有个退出条件：
2. if not node.right and not node.left:
   1. return levels

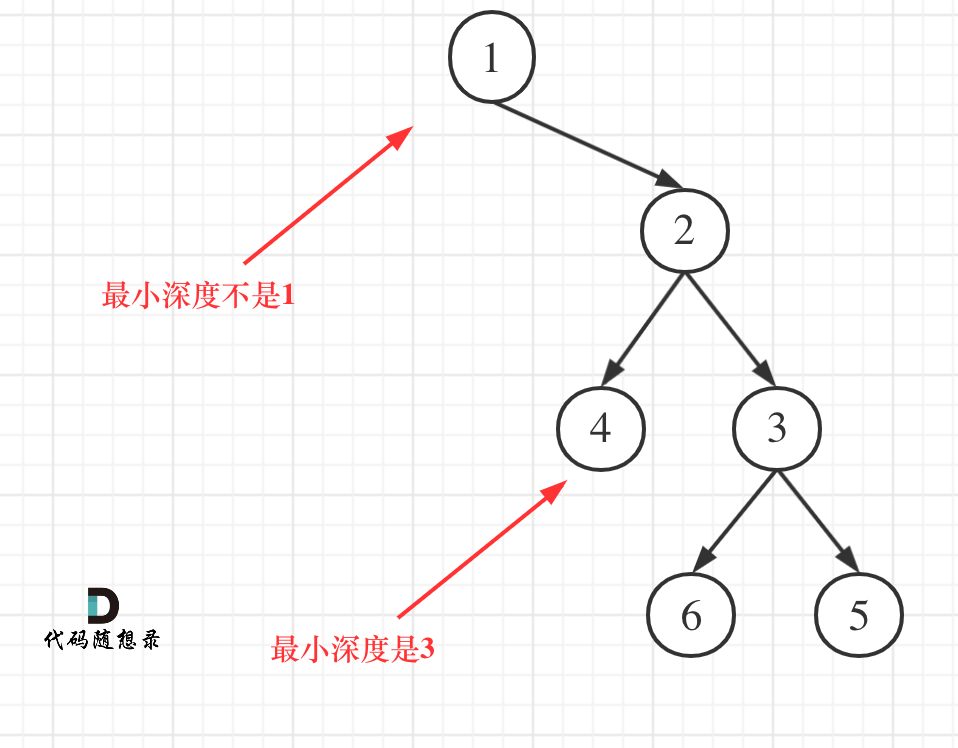
不加这行就报错，因为那样就会变成求最大深度了而不是“最小深度”

比如这个例子，如果不加这行，会输出3而不是2

迭代代码

def minDepth(self, root: Optional[TreeNode]) -> int:
    # 使用迭代法（层序）
    from collections import deque

    que = deque()
    if not root:
        return 0
    que.append(root)
    levels = 0
    while que:
        L = len(que)
        levels += 1
        for i in range(L):
            node = que.popleft()
            if node.left:
                que.append(node.left)
            if node.right:
                que.append(node.right)
            # 当左右孩子都为空的时候，说明是最低点的一层了，退出
            # 不加这行就报错，因为那样就会变成求最大深度了而不是“最小深度”
            if not node.right and not node.left:
                return levels
    return levels