LeetCodeCampsDay28贪心part02
LeetCodeCampsDay28贪心part02
覆盖范围的题目
122. 买卖股票的最佳时机 II
https://leetcode.cn/problems/best-time-to-buy-and-sell-stock-ii/
给你一个整数数组 prices ,其中 prices[i] 表示某支股票第 i 天的价格。
在每一天,你可以决定是否购买和/或出售股票。你在任何时候 最多 只能持有 一股 股票。你也可以先购买,然后在 同一天 出售。
返回 你能获得的 最大 利润 。
示例 1:
1 | 输入:prices = [7,1,5,3,6,4] |
示例 2:
1 | 输入:prices = [1,2,3,4,5] |
示例 3:
1 | 输入:prices = [7,6,4,3,1] |
提示:
1 <= prices.length <= 3 * 1040 <= prices[i] <= 104
贪心思路
观察例子可以看到,
1 | 输入:prices = [1,2,3,4,5] |
虽然解释是第一天买,最后一天卖;但第一天买,第二天卖,第二天再买,第三天卖……最终也会得到同样的利润。因为把利润分解为每天为单位的维度,而不是从 1 天到第 5 天整体去考虑!
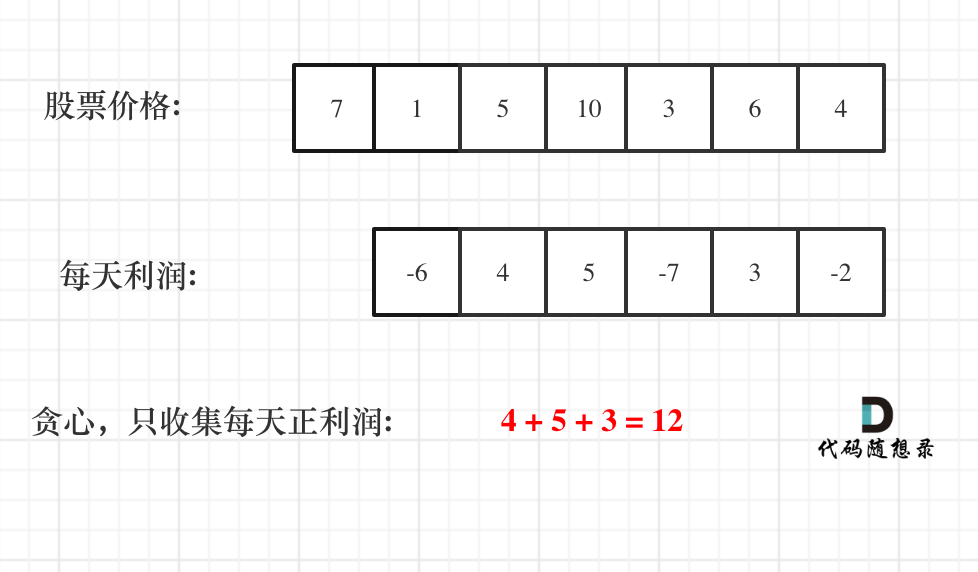
所以,我们可以算出每天的利润表
1 | prices = [7,1,5,3,6,4] |
只统计DailProfit里大于零的利润就好了
那?第一天怎么就没有利润呢,第一天到底算不算的困惑中。
第一天当然没有利润,至少要第二天才会有利润,所以利润的序列比股票序列少一天!
从图中可以发现,其实我们需要收集每天的正利润就可以,收集正利润的区间,就是股票买卖的区间,而我们只需要关注最终利润,不需要记录区间。
那么只收集正利润就是贪心所贪的地方!
局部最优:收集每天的正利润,全局最优:求得最大利润。
贪心代码
- 时间复杂度O(N)
- 空间复杂度O(1)
1 | class Solution: |
55. 跳跃游戏
https://leetcode.cn/problems/jump-game/
给你一个非负整数数组 nums ,你最初位于数组的 第一个下标 。数组中的每个元素代表你在该位置可以跳跃的最大长度。
判断你是否能够到达最后一个下标,如果可以,返回 true ;否则,返回 false 。
示例 1:
1 | 输入:nums = [2,3,1,1,4] |
示例 2:
1 | 输入:nums = [3,2,1,0,4] |
提示:
1 <= nums.length <= 1040 <= nums[i] <= 105
贪心思路
本题其实跳几步无所谓,关键在于可跳的覆盖范围!
贪心代码
- 时间复杂度O(N)
- 空间复杂度O(1)
1 | L = len(nums) |
分治思路
数值:[2,3,1,1,4]
下标:[0,1,2,3,4]
从末尾向前检查,设置当前位置(cur)是最后一位,如果当前位置到i的距离(cur - i)小于等于nums[i],说明当前位置可以被访问,最终判断cur是否回到了0
这种方法最好就是从终点走回到起点,逐渐将一个[2,3,1,1,4]的问题变成[2,3,1,1]->[2,3,1]->[2,3]->[2]
分治代码
- 时间复杂度O(N)
- 空间复杂度O(1)
1 | class Solution: |
动态规划
设置个stepsAvailable,表示从当前位置能走的最大步数,一步步模拟,如果某个位置的nums[i]大于stepsAvailable,则更新stepsAvailable=nums[i]
动态规划代码
- 时间复杂度O(N)
- 空间复杂度O(1)
1 | L = len(nums) |
45. 跳跃游戏 II
https://leetcode.cn/problems/jump-game-ii/
给定一个长度为 n 的 0 索引整数数组 nums。初始位置为 nums[0]。
每个元素 nums[i] 表示从索引 i 向后跳转的最大长度。换句话说,如果你在 nums[i] 处,你可以跳转到任意 nums[i + j] 处:
0 <= j <= nums[i]i + j < n
返回到达 nums[n - 1] 的最小跳跃次数。生成的测试用例可以到达 nums[n - 1]。
示例 1:
1 | 输入: nums = [2,3,1,1,4] |
示例 2:
1 | 输入: nums = [2,3,0,1,4] |
提示:
1 <= nums.length <= 1040 <= nums[i] <= 1000- 题目保证可以到达
nums[n-1]
贪心思路
贪心的思路,局部最优:当前可移动距离尽可能多走,如果还没到终点,步数再加一。整体最优:一步尽可能多走,从而达到最少步数。
思路虽然是这样,但在写代码的时候还不能真的能跳多远就跳多远,那样就不知道下一步最远能跳到哪里了。
所以真正解题的时候,要从覆盖范围出发,不管怎么跳,覆盖范围内一定是可以跳到的,以最小的步数增加覆盖范围,覆盖范围一旦覆盖了终点,得到的就是最少步数!
这里需要统计两个覆盖范围,当前这一步的最大覆盖和下一步最大覆盖。
如果移动下标达到了当前这一步的最大覆盖最远距离了,还没有到终点的话,那么就必须再走一步来增加覆盖范围,直到覆盖范围覆盖了终点。
我们每次在可跳范围内选择可以使得跳的更远的位置。
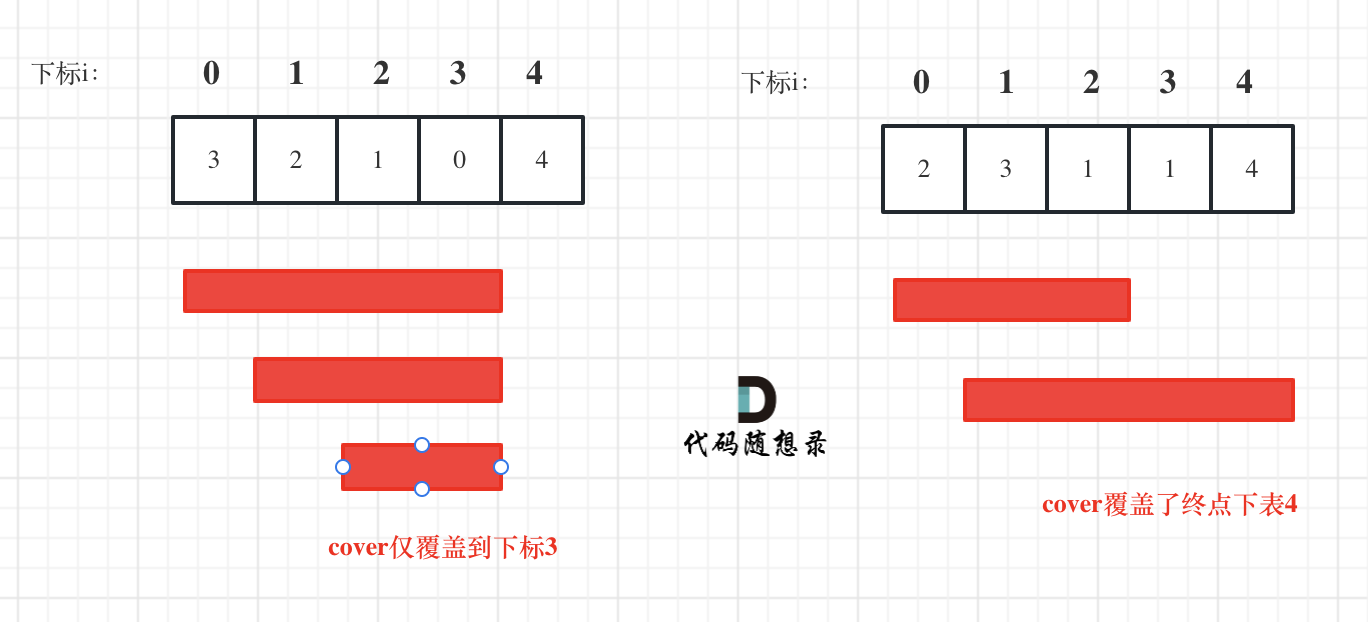
如下图,开始的位置是 2,可跳的范围是橙色的。然后因为 3 可以跳的更远,所以跳到 3 的位置。
如下图,然后现在的位置就是 3 了,能跳的范围是橙色的,然后因为 4 可以跳的更远,所以下次跳到 4 的位置。
在代码里,我们用 end 表示当前能跳的边界,对于上边第一个图的橙色 1,第二个图中就是橙色的 4,遍历数组的时候,到了边界,我们就重新更新新的边界。
贪心代码
- 时间复杂度O(N)
- 空间复杂度O(1)
1 | class Solution: |
1005. K 次取反后最大化的数组和
https://leetcode.cn/problems/maximize-sum-of-array-after-k-negations/
给你一个整数数组 nums 和一个整数 k ,按以下方法修改该数组:
- 选择某个下标
i并将nums[i]替换为-nums[i]。
重复这个过程恰好 k 次。可以多次选择同一个下标 i 。
以这种方式修改数组后,返回数组 可能的最大和 。
示例 1:
1 | 输入:nums = [4,2,3], k = 1 |
示例 2:
1 | 输入:nums = [3,-1,0,2], k = 3 |
示例 3:
1 | 输入:nums = [2,-3,-1,5,-4], k = 2 |
提示:
1 <= nums.length <= 104-100 <= nums[i] <= 1001 <= k <= 104
贪心思路
先将nums排序,按绝对值排序,从大到小
再对小于0的数字进行反转,每次消耗一次k
如果k有剩余,就对着最小的数进行反转剩下的k次(不过按奇偶划分下就行,偶数就不用反转,奇数就反转一次)
贪心代码
- 时间复杂度O(N)
- 空间复杂度O(1)
1 | class Solution: |