LeetCodeCampsDay34动态规划part02

62. 不同路径

https://leetcode.cn/problems/unique-paths/

一个机器人位于一个 m x n 网格的左上角 （起始点在下图中标记为 “Start” ）。

机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为 “Finish” ）。

问总共有多少条不同的路径？

示例 1：

img

1
2
输入：m = 3, n = 7
输出：28

示例 2：

1
2
3
4
5
6
7
输入：m = 3, n = 2
输出：3
解释：
从左上角开始，总共有 3 条路径可以到达右下角。
1. 向右 -> 向下 -> 向下
2. 向下 -> 向下 -> 向右
3. 向下 -> 向右 -> 向下

示例 3：

1
2
输入：m = 7, n = 3
输出：28

示例 4：

1
2
输入：m = 3, n = 3
输出：6

提示：

  • 1 <= m, n <= 100
  • 题目数据保证答案小于等于 2 * 109

动态规划思路

dp下标与数组含义: 一维数组即可，下标指地图下标，数组含意到达当前位置的路径数

递推公式：当前位置的路径数dp[i]=dp[i](上一行的）+dp[i-1]

初始化：全初始化为1

遍历顺序，从下标(1,1)开始遍历，到n-1结束，输出dp[n-1]，跳过第一行和第一列

1,1,1,1,1,1,1

1,2,3,4,5,6,7

1,3,6,10,15,21,28

动态规划代码

1
2
3
4
5
6
7
8
class Solution:
    def uniquePaths(self, m: int, n: int) -> int:
        dp = [1] * n
        # 跳过第一行和第一列
        for _ in  range(1, m):
            for i in range(1, n):
                dp[i] += dp[i-1]
        return dp[n-1]

63. 不同路径 II

https://leetcode.cn/problems/unique-paths-ii/

给定一个 m x n 的整数数组 grid。一个机器人初始位于 左上角（即 grid[0][0]）。机器人尝试移动到 右下角（即 grid[m - 1][n - 1]）。机器人每次只能向下或者向右移动一步。

网格中的障碍物和空位置分别用 1 和 0 来表示。机器人的移动路径中不能包含 任何 有障碍物的方格。

返回机器人能够到达右下角的不同路径数量。

测试用例保证答案小于等于 2 * 109。

示例 1：

img

1
2
3
4
5
6
输入：obstacleGrid = [[0,0,0],[0,1,0],[0,0,0]]
输出：2
解释：3x3 网格的正中间有一个障碍物。
从左上角到右下角一共有 2 条不同的路径：
1. 向右 -> 向右 -> 向下 -> 向下
2. 向下 -> 向下 -> 向右 -> 向右

示例 2：

img

1
2
输入：obstacleGrid = [[0,1],[0,0]]
输出：1

提示：

  • m == obstacleGrid.length
  • n == obstacleGrid[i].length
  • 1 <= m, n <= 100
  • obstacleGrid[i][j] 为 0 或 1

动态规划思路

dp下标与含义, dp一维数组，下标是地图下标；含义当前位置的路径数

递推公式：如果当前位置可到达，则dp[i]=dp[i]+dp[i-1]，不可到达则为0

dp初始化，按顺序初始化，如果遇到obstacle就停止初始化

遍历顺序，跳过第一行、每列从0遍历到n-1

obstacle

1,1,1,x,1,1

1,1,x,1,1,1

1,1,1,1,1,1

下面是dp

1,1,1,0,0,0

1,2,0,0,0,0

1,3,3,3,3,3

动态规划代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class Solution:
    def uniquePathsWithObstacles(self, obstacleGrid: List[List[int]]) -> int:
        Lrows = len(obstacleGrid)
        Lcols = len(obstacleGrid[0])
        dp = [0] * Lcols
        for i in range(Lcols):
            if obstacleGrid[0][i] == 1:
                break
            dp[i] = 1

        for i in range(1, Lrows):
            # 每列从0开始
            for j in range(Lcols):
                if obstacleGrid[i][j] == 1:
                    dp[j] = 0
                elif j != 0 :
                    dp[j] += dp[j-1]

        return dp[Lcols - 1]

343. 整数拆分

https://leetcode.cn/problems/integer-break/

给定一个正整数 n ，将其拆分为 k 个 正整数 的和（ k >= 2 ），并使这些整数的乘积最大化。

返回 你可以获得的最大乘积 。

示例 1:

1
2
3
输入: n = 2
输出: 1
解释: 2 = 1 + 1, 1 × 1 = 1。

示例 2:

1
2
3
输入: n = 10
输出: 36
解释: 10 = 3 + 3 + 4, 3 × 3 × 4 = 36。

提示:

  • 2 <= n <= 58

动态规划思路

  1. dp数组下标是数字i，dp[i]是数字i的最大乘积

dp[i]：分拆数字i，可以得到的最大乘积为dp[i]。

dp[i]的定义将贯彻整个解题过程，下面哪一步想不懂了，就想想dp[i]究竟表示的是啥！

将数字i拆分成(i-j)和j两个部分，其中j \in (1, i-1)，或者j和dp[i-j]三及个以上部分，分成这两种情况，判断两种情况的最大值，即max((i -j ) * j, dp[i - j] * j)

  1. 递推公式：dp[i] = max(dp[i], max((i -j ) * j, dp[i - j] * j)) ，因为每次都需要让max((i -j ) * j, dp[i - j] * j)再和dp[i]比较，找到最大值

  2. 初始化：dp[0]和dp[1]不用初始化（因为没有意义），或者直接初始化为1也可以通过,其它的全部初始化为1

  3. 遍历顺序：i从2到n, j从1到i-1

  4. dp举例：
    n = 10
    i=2, j=1, dp[2] = max(dp[2], max(1*1, 1*dp[1])) ,dp[2] = 1
    i=3, j=1, dp[3] = max(dp[3], max(1*2, 1*dp[2])) ,dp[3] = 2
    i=3, j=2, dp[3] = max(dp[3], max(2*1, 2*dp[1])) ,dp[3] = 2
    i=4, j=1, dp[4] = max(dp[4], max(1*3, 1*dp[3])), dp[4] = 3
    i=4, j=2, dp[4] = max(dp[4], max(2*2, 2*dp[2])), dp[4] = 4
    i=4, j=3, dp[4] = max(dp[4], max(3*1, 3*dp[1])), dp[4] = 4
    i=5, j=1, dp[5] = max(dp[5], max(1*4, 1*dp[4])), dp[5] = 4
    i=5, j=2, dp[5] = max(dp[5], max(2*3, 2*dp[3])), dp[5] = 6

因为拆分一个数n 使之乘积最大，那么一定是拆分成m个近似相同的子数相乘才是最大的。

例如 6 拆成 3 * 3， 10 拆成 3 * 3 * 4。 100的话 也是拆成m个近似数组的子数 相乘才是最大的。

只不过我们不知道m究竟是多少而已，但可以明确的是m一定大于等于2，既然m大于等于2，也就是 最差也应该是拆成两个相同的 可能是最大值。

那么 j 遍历，只需要遍历到 n//2（包含） 就可以，后面就没有必要遍历了，一定不是最大值。

动态规划代码

1
2
3
4
5
6
7
8
9
10
class Solution:
    def integerBreak(self, n: int) -> int:
       	# 因为包含了0所以是n+1
        dp = [1] * (n + 1)
        for i in range(2, n + 1):
          	# 不优化则是1, i；优化则是1, i//2 + 1
            for j in range(1, i//2 + 1):
                dp[i] = max(dp[i], max(j * (i - j), j * dp[i - j]))
        return dp[-1]

96. 不同的二叉搜索树

https://leetcode.cn/problems/unique-binary-search-trees/

给你一个整数 n ，求恰由 n 个节点组成且节点值从 1 到 n 互不相同的 二叉搜索树 有多少种？返回满足题意的二叉搜索树的种数。

示例 1：

img

1
2
输入：n = 3
输出：5

示例 2：

1
2
输入：n = 1
输出：1

提示：

  • 1 <= n <= 19

动态规划思路

dp数组下标是整数i， dp[i]表示有dp[i]个不同的二叉搜索树

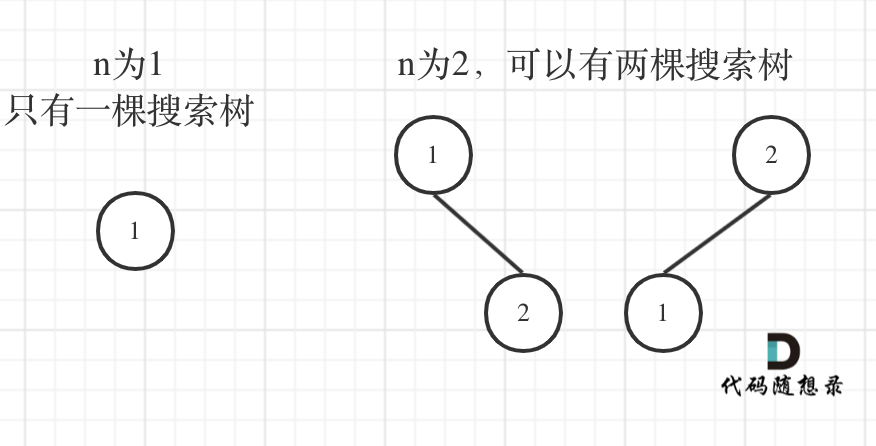
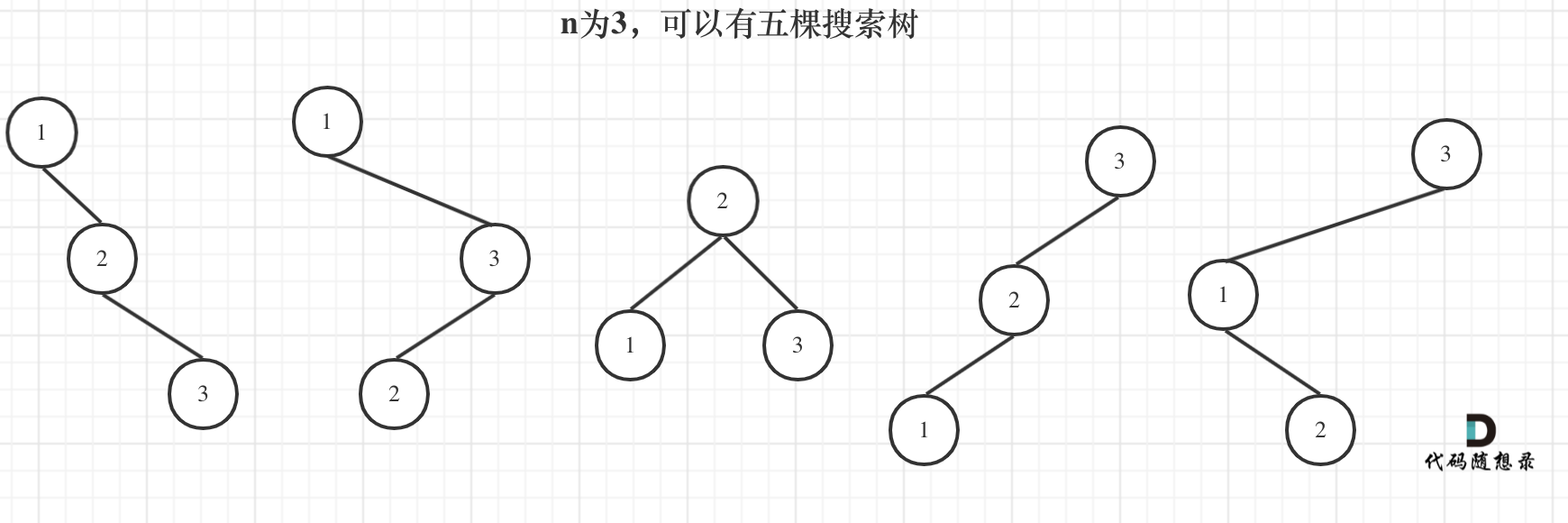
递推公式，若n=3, 有三种情况，root=1, 左子树有0节点，右子树有2个节点；root=2, 左子树有1节点，右子树有1节点；root=3，左子树有2节点，右子树0节点

img

img

dp[3] = dp[0] * dp[2] + dp[1] * dp[1] + dp[2] * dp[0]

img

dp[i] = dp[i] + dp[j-1](左子树) * dp[i-j]（右子树），其中j为root

初始化，dp[0]=1, dp[1]=1

遍历顺序，行遍历, i从2到n；列遍历，j从0到i-1，j表示左子树的数量

举例如上

动态规划代码

1
2
3
4
5
6
7
8
9
10
11
class Solution:
    def numTrees(self, n: int) -> int:
        # 
        dp = [0] * (n + 1)
        dp[0] = dp[1] = 1

        for i in range(2, n + 1):
            for j in range(i):
                dp[i] = dp[i] + dp[j] * dp[i - j - 1]
        return dp[-1]

额外题目

11. 盛最多水的容器

https://leetcode.cn/problems/container-with-most-water/

给定一个长度为 n 的整数数组 height 。有 n 条垂线，第 i 条线的两个端点是 (i, 0) 和 (i, height[i]) 。

找出其中的两条线，使得它们与 x 轴共同构成的容器可以容纳最多的水。

返回容器可以储存的最大水量。

**说明：**你不能倾斜容器。

示例 1：

img

1
2
3
输入：[1,8,6,2,5,4,8,3,7]
输出：49 
解释：图中垂直线代表输入数组 [1,8,6,2,5,4,8,3,7]。在此情况下，容器能够容纳水（表示为蓝色部分）的最大值为 49。

示例 2：

1
2
输入：height = [1,1]
输出：1

提示：

  • n == height.length
  • 2 <= n <= 105
  • 0 <= height[i] <= 104

双指针思路

观察得知，区间的面积=底宽*两端最小高度

左指针从左向右，右指针反向；判断两个指针所在高度，并移动低高度的指针

双指针代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
class Solution:
    def maxArea(self, height: List[int]) -> int:
        # 双指针
        lP = 0
        rP = len(height) - 1
        res = 0
        while lP < rP:
            if height[lP] < height[rP]:
                res = max(res, (rP - lP) * height[lP])
                lP += 1
            else:
                res = max(res, (rP - lP) * height[rP])
                rP -= 1

        return res

167. 两数之和 II - 输入有序数组

https://leetcode.cn/problems/two-sum-ii-input-array-is-sorted/

给你一个下标从 1 开始的整数数组 numbers ，该数组已按 非递减顺序排列 ，请你从数组中找出满足相加之和等于目标数 target 的两个数。如果设这两个数分别是 numbers[index1] 和 numbers[index2] ，则 1 <= index1 < index2 <= numbers.length 。

以长度为 2 的整数数组 [index1, index2] 的形式返回这两个整数的下标 index1 和 index2。

你可以假设每个输入 只对应唯一的答案 ，而且你 不可以 重复使用相同的元素。

你所设计的解决方案必须只使用常量级的额外空间。

示例 1：

1
2
3
输入：numbers = [2,7,11,15], target = 9
输出：[1,2]
解释：2 与 7 之和等于目标数 9 。因此 index1 = 1, index2 = 2 。返回 [1, 2] 。

示例 2：

1
2
3
输入：numbers = [2,3,4], target = 6
输出：[1,3]
解释：2 与 4 之和等于目标数 6 。因此 index1 = 1, index2 = 3 。返回 [1, 3] 。

示例 3：

1
2
3
输入：numbers = [-1,0], target = -1
输出：[1,2]
解释：-1 与 0 之和等于目标数 -1 。因此 index1 = 1, index2 = 2 。返回 [1, 2] 。

提示：

  • 2 <= numbers.length <= 3 * 104
  • -1000 <= numbers[i] <= 1000
  • numbers 按 非递减顺序 排列
  • -1000 <= target <= 1000
  • 仅存在一个有效答案

双指针思路

本题目已经排序好了，可以直接双指针，一个指针从左向右；另一从右向左；

如果现指针之和大于target，右指针向左；如果小于target，左指针向右；直到相等

双指针代码

  • 时间复杂度O(N)
  • 空间复杂度O(1)—前提是有序
1
2
3
4
5
6
7
8
9
10
11
12
13
14
class Solution:
    def twoSum(self, numbers: List[int], target: int) -> List[int]:
        # 用hashtable或者双指针
        # 
        lP = 0
        rP = len(numbers) - 1
        while lP < rP:
            if numbers[lP] + numbers[rP] < target:
                lP += 1
            elif numbers[lP] + numbers[rP] > target:
                rP -= 1
            else:
                return lP + 1, rP + 1
        return

hash思路

可以只遍历一遍，但借用hashtable，将target - nums[i]装到table里,并每次遍历时在nums里找是否已经出现在table里，是则找到了两个值

hash代码

  • 时间复杂度O(N)
  • 空间复杂度O(N)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
class Solution:
    def twoSum(self, numbers: List[int], target: int) -> List[int]:
        # 用hashtable或者双指针


        # 如果用hashtable，
        table = dict()
        L = len(numbers)
        for i in range(L):
            if numbers[i] not in table:
                table[target - numbers[i]] = i
            else:
                return table[numbers[i]] + 1, i + 1
        return

3. 无重复字符的最长子串

https://leetcode.cn/problems/longest-substring-without-repeating-characters/

给定一个字符串 s ，请你找出其中不含有重复字符的 最长 子串 的长度。

示例 1:

1
2
3
输入: s = "abcabcbb"
输出: 3 
解释: 因为无重复字符的最长子串是 "abc"，所以其长度为 3。

示例 2:

1
2
3
输入: s = "bbbbb"
输出: 1
解释: 因为无重复字符的最长子串是 "b"，所以其长度为 1。

示例 3:

1
2
3
4
输入: s = "pwwkew"
输出: 3
解释: 因为无重复字符的最长子串是 "wke"，所以其长度为 3。
     请注意，你的答案必须是 子串 的长度，"pwke" 是一个子序列，不是子串。

提示：

  • 0 <= s.length <= 5 * 104
  • s 由英文字母、数字、符号和空格组成

双指针结合hash思路

建立一个hashtable记录出现的字符所在下标，如果遇到了个重复的字符s[i]，那么新的子串开始位置一定是从table[s[i]] + 1开始

如果没遇到重复的，则将table[s[i]]设置为下标i，并且更新最长子段长度

注意：新的子串开始位置一定是从table[s[i]] + 1开始 那旧的子串在table里的值是否需要被删除？

答：不需要真的去删除它，但需要在判断时，添加一个条件table[s[right]] >= left，注意这里的left是子串开始的下标

双指针结合hash代码

  • 时间复杂度O(N)
  • 空间复杂度O(min(n, m))，m是字符集大小
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
class Solution:
    def lengthOfLongestSubstring(self, s: str) -> int:
        # 如果遇到重复，从子串中重复字母的下一个开始作为新子串

        # 使用hashtable
        table = dict()
        L = len(s)
        left = 0
        res = 0
        for right in range(L):
            # 遇到重复
            if s[right] in table and table[s[right]] >= left:
                left = table[s[right]] + 1
            table[s[right]] = right
            res = max(res,  right - left + 1)
        return res