LeetCodeCampsDay35动态规划part03

背包问题/01背包/一维dp数组与二维dp数组的执行区别

背包问题

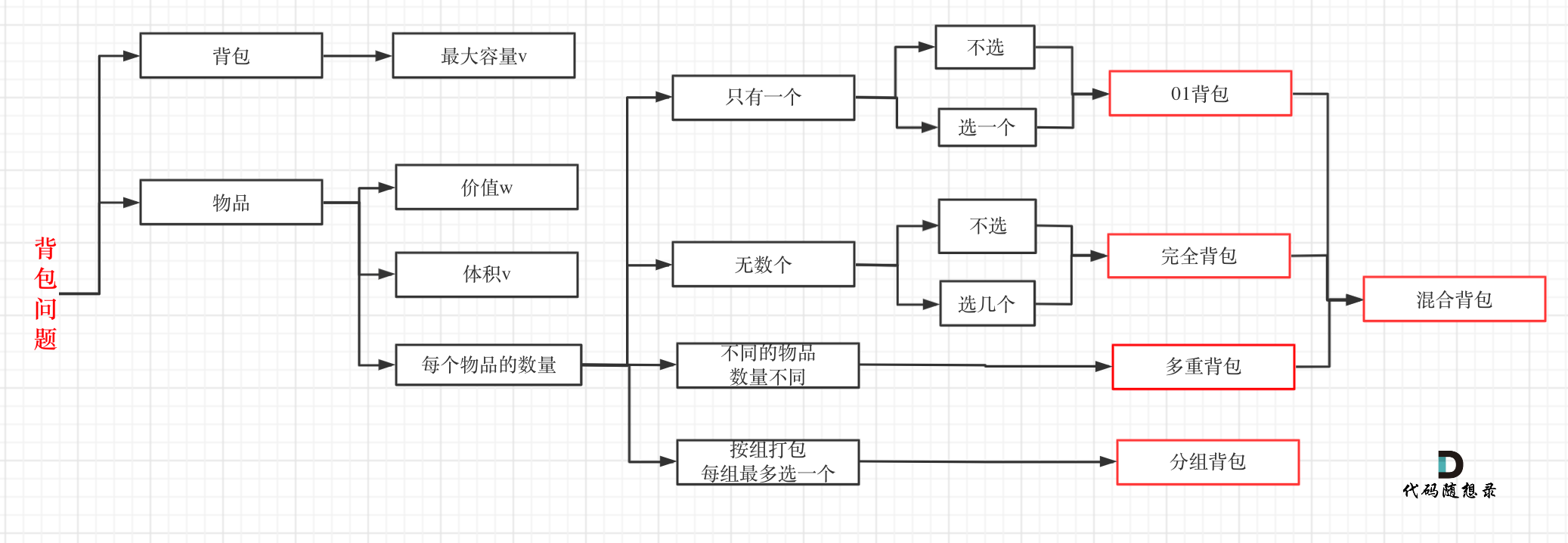
背包问题可以分成01背包/完全背包/多重背包与分组背包；

不过搞定01背包与完全背包就可以了

01背包

有n件物品和一个最多能背重量为w 的背包。

第i件物品的重量是weight[i]，得到的价值是value[i] 。每件物品只能用一次，求解将哪些物品装入背包里物品价值总和最大。

这是标准的背包问题，以至于很多同学看了这个自然就会想到背包，甚至都不知道暴力的解法应该怎么解了。

这样其实是没有从底向上去思考，而是习惯性想到了背包，那么暴力的解法应该是怎么样的呢？

每一件物品其实只有两个状态，取或者不取 ，所以可以使用回溯法搜索出所有的情况，那么时间复杂度就是O(2^n)，这里的n表示物品数量。

所以暴力的解法是指数级别的时间复杂度。进而才需要动态规划的解法来进行优化！

在下面的讲解中，我举一个例子：

背包最大重量为4。

物品为：

	重量	价值
物品0	1	15
物品1	3	20
物品2	4	30

问背包能背的物品最大价值是多少？

以下讲解和图示中出现的数字都是以这个例子为例。

（为了方便表述，下面描述 统一用 容量为XX的背包，放下容量（重量）为XX的物品，物品的价值是XX）

二维数组01背包

1. 先确定dp数组下标与数组含义

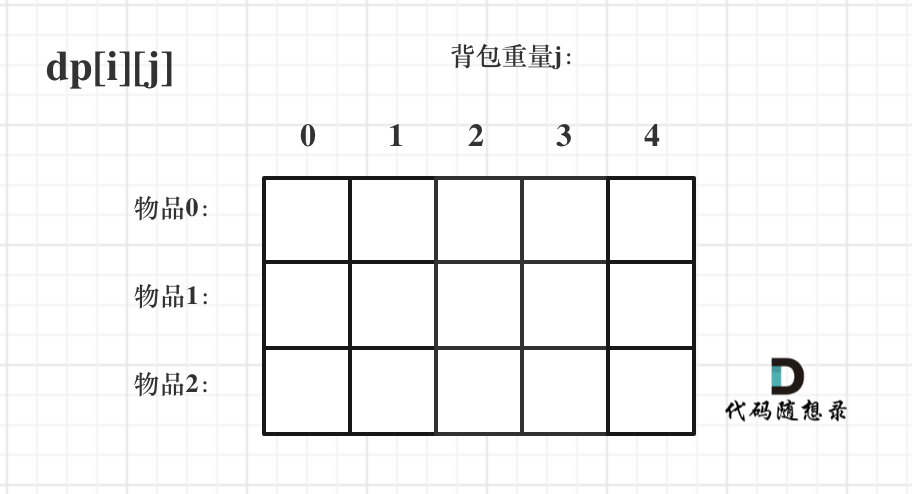
因为我们需要同时表示 物品 & 背包容量，所以dp[i][j]里的i表示物品i，而j表示当前背包容量为j，注意如果背包capacity为4，但dp数组的长度需要开到5，因为包含重量为0的情况

动态规划的思路是根据子问题的求解推导出整体的最优解

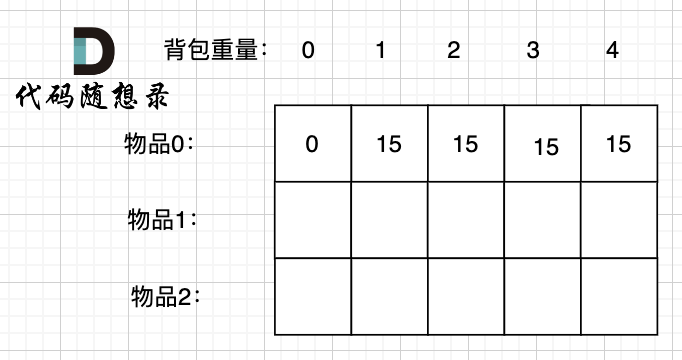
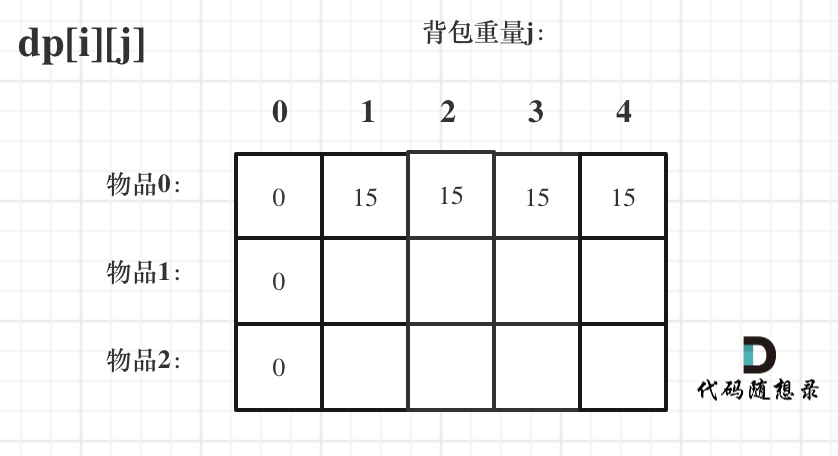
先把物品0放在背包里

背包容量为0，放不下物品0，此时背包里的价值为0。

背包容量为1，可以放下物品0，此时背包里的价值为15.

背包容量为2，依然可以放下物品0 （注意 01背包里物品只有一个），此时背包里的价值为15。

以此类推。

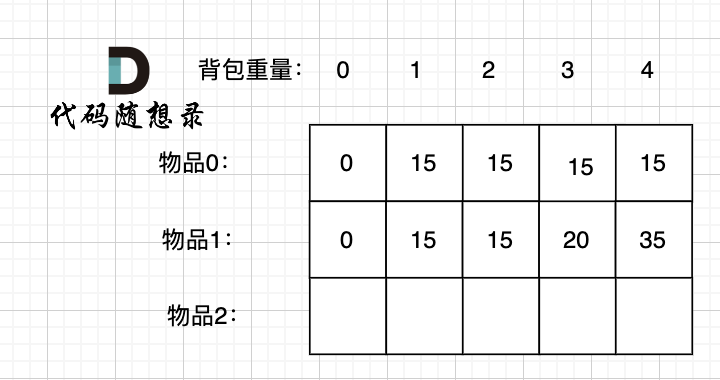
再看把物品1 放入背包：

背包容量为 0，放不下物品0 或者物品1，此时背包里的价值为0。

背包容量为 1，只能放下物品0，背包里的价值为15。

背包容量为 2，只能放下物品0，背包里的价值为15。

背包容量为 3，上一行同一状态，背包只能放物品0，这次也可以选择物品1了，背包可以放物品1 或者 物品0 ，物品1价值更大，背包里的价值为20

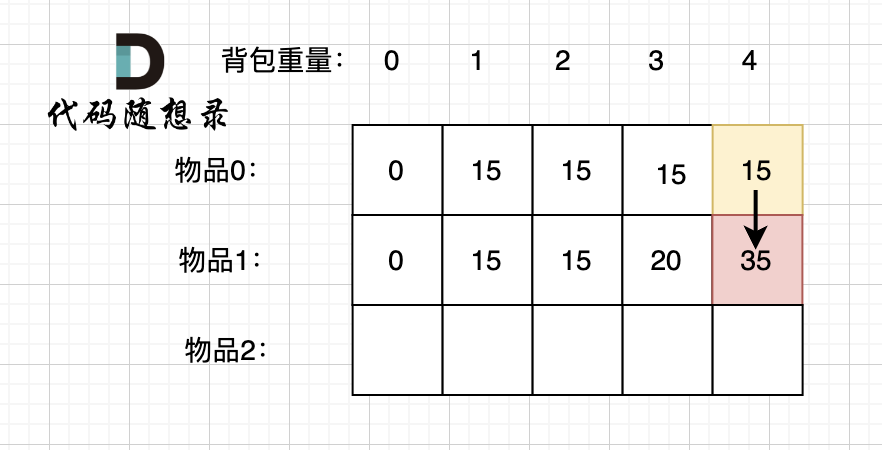
背包容量为 4，上一行同一状态，背包只能放物品0，这次也可以选择物品1了，背包可以放下物品0 和 物品1 ，背包价值为35

2. 对于递推公式，首先我们要明确有哪些方向可以推导出 dp[i][j]。

这里我们dp[1][4]的状态来举例：

求取 dp[1][4] 有两种情况：

1. 放物品1
2. 还是不放物品1

如果不放物品1， 那么背包的价值应该是 dp[0][4] 即 容量为4的背包，只放物品0的情况。

如果放物品1， 那么背包要先留出物品1的容量，目前容量是4，物品1 的容量（就是物品1的重量）为3，此时背包剩下容量为1。

容量为1，只考虑放物品0 的最大价值是 dp[0][1]，这个值我们之前就计算过。

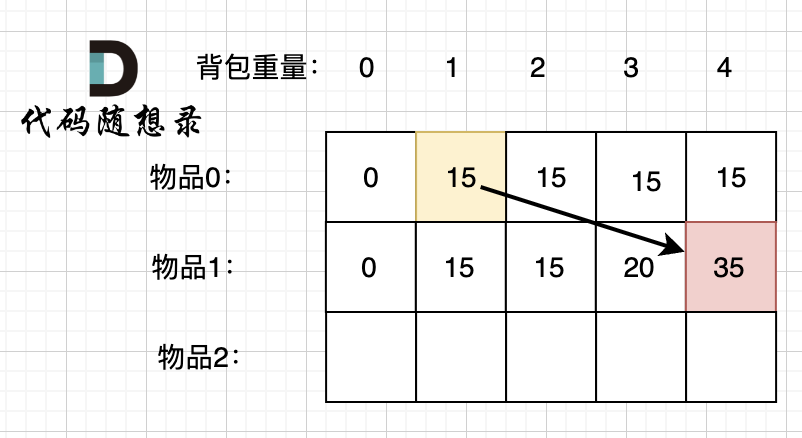
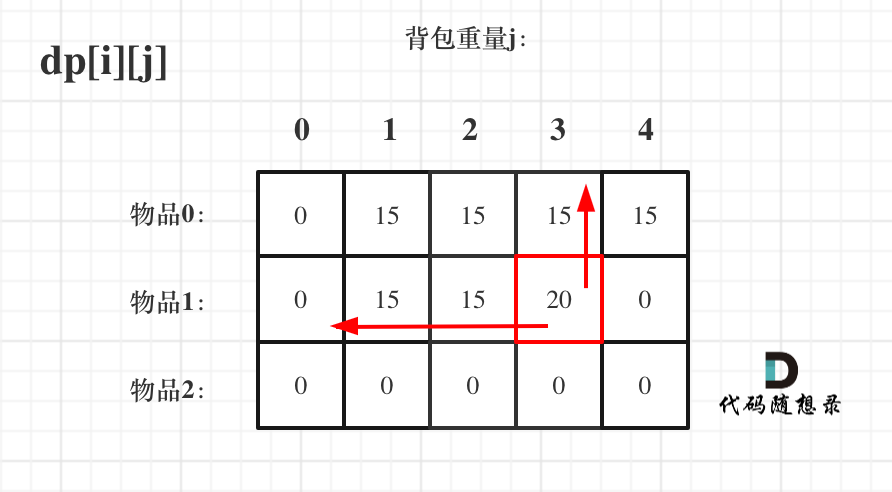
所以 放物品1 的情况 = dp[0][1] + 物品1 的价值，推导方向如图：

两种情况，分别是放物品1 和 不放物品1，我们要取最大值（毕竟求的是最大价值）

dp[1][4] = max(dp[0][4], dp[0][1] + 物品1 的价值)

以上过程，抽象化如下：

• 不放物品i：背包容量为j，里面不放物品i的最大价值是dp[i - 1][j]。
• 放物品i：背包空出物品i的容量后，背包容量为j - weight[i]，dp[i - 1][j - weight[i]] 为背包容量为j - weight[i]且不放物品i的最大价值，那么dp[i - 1][j - weight[i]] + value[i] （物品i的价值），就是背包放物品i得到的最大价值

递归公式： dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);

3. dp数组初始化

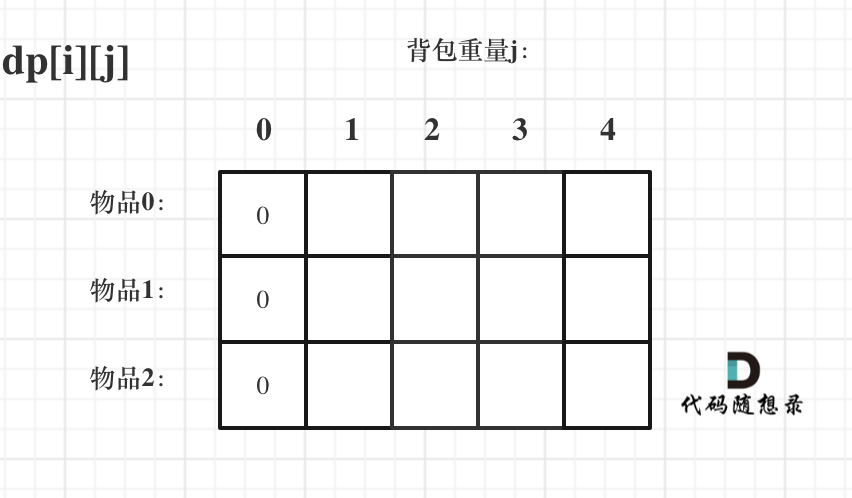
首先从dp[i][j]的定义出发，如果背包容量j为0的话，即dp[i][0]，无论是选取哪些物品，背包价值总和一定为0。如图：

状态转移方程 dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]); 可以看出i 是由 i-1 推导出来，那么i为0的时候就一定要初始化。

dp[0][j]，即：i为0，存放编号0的物品的时候，各个容量的背包所能存放的最大价值。

那么很明显当 j < weight[0]的时候，dp[0][j] 应该是 0，因为背包容量比编号0的物品重量还小。

当j >= weight[0]时，dp[0][j] 应该是value[0]，因为背包容量放足够放编号0物品。

# 这里是正序遍历
for (int j = weight[0]; j <= bagweight; j++) {
    dp[0][j] = value[0];
}

而其实位置的dp数据初始化为什么都可以，因为它们会在计算时被直接覆盖掉，所以全部初始化为0

4. 遍历顺序

明显有两个维度 ：物品个数 与 背包容量，我们先遍历物品个数再遍历背包容量

// weight数组的大小 就是物品个数
for(int i = 1; i < weight.size(); i++) { // 遍历物品
    for(int j = 0; j <= bagweight; j++) { // 遍历背包容量
        if (j < weight[i]) dp[i][j] = dp[i - 1][j];
        else dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);

    }
}

先遍历背包容量再物品个数

// weight数组的大小 就是物品个数
for(int j = 0; j <= bagweight; j++) { // 遍历背包容量
    for(int i = 1; i < weight.size(); i++) { // 遍历物品
        if (j < weight[i]) dp[i][j] = dp[i - 1][j];
        else dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);
    }
}

虽然两个for循环遍历的次序不同，但是dp[i][j]所需要的数据就是左上角，根本不影响dp[i][j]公式的推导！

但先遍历物品再遍历背包这个顺序更好理解。

其实背包问题里，两个for循环的先后循序是非常有讲究的，理解遍历顺序其实比理解推导公式难多了。

5. 举例推导dp数组

这里在把基本信息给出来：

	重量	价值
物品0	1	15
物品1	3	20
物品2	4	30

从物品1开始遍历，背包容量从0开始遍历

0<weight[1]: dp[1][0] = dp[0][0] = 15

1<weight[1]: dp[1][1] = dp[0][1] = 15

2<weight[1]: dp[1][2] = dp[0][2] = 15

3>=weight[1]: dp[1][3] = max(dp[0][3], dp[0][3 - weight[1]] + val[1]) = 20

4>=weight[1]: dp[1][4] = max(dp[0][4], dp[0][4 - weight[1]] + val[1]) = 35

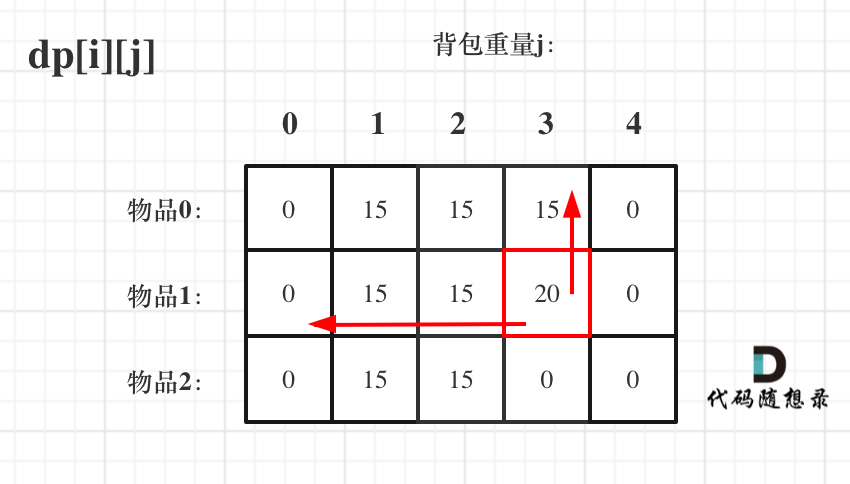
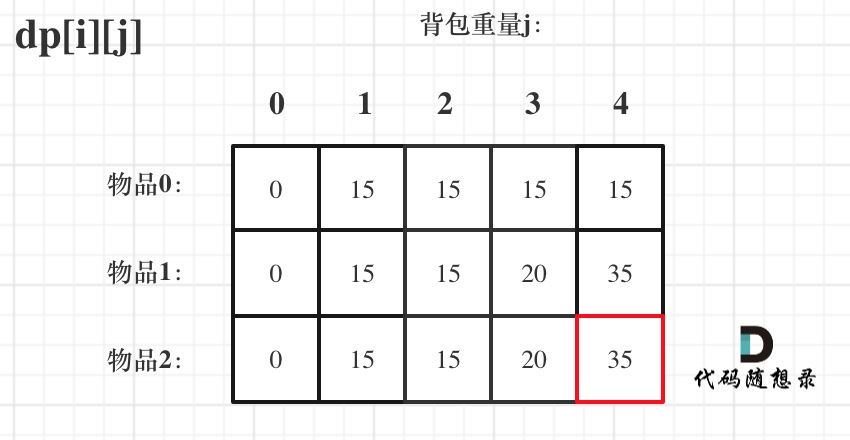
再遍历物品2，仍然从容量0开始遍历

一维数组01背包

递推公式如下：dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + val[i])

可见dp每次会用到上一个物品dp[i-1]的值，而我们完全可以用一个一维数组，表示每个物品在不同背包容量下的最大价值；

dp[j] = max(dp[j], dp[j - weight[i]] + val[i])

max里的的dp[j]和dp[j - weight[i]] 其实是上一个物品i的值，新一个物品i+1的值是最左边的dp[j]

一维数组遍历时与二维数组不同

一维dp数组遍历顺序代码如下：

for(int i = 0; i < weight.size(); i++) { // 遍历物品
    for(int j = bagWeight; j >= weight[i]; j--) { // 遍历背包容量
        dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);

    }
}

这里大家发现和二维dp的写法中，遍历背包的顺序是不一样的！

二维dp遍历的时候，背包容量是从小到大，而一维dp遍历的时候，背包是从大到小。

为什么呢？

倒序遍历是为了保证物品i只被放入一次！。但如果一旦正序遍历了，那么物品0就会被重复加入多次！

举一个例子：物品0的重量weight[0] = 1，价值value[0] = 15

如果正序遍历

dp[1] = max(dp[1 - weight[0]] + value[0], dp[1]) = 15

dp[2] = max(dp[2 - weight[0]] + value[0], dp[2]) = 30（因为value[0]=15,而dp[2 - weight[0]]=15）

比如下表是在计算dp[2]时的情况

	0	1	2	3	4
物品0	0	0	0	0	0
物品1	0	15

在计算dp[2]时，max(dp[2 - weight[0]] + value[0], dp[2]) 里 dp[2 - weight[0]]的本意是拿(物品0, 下标1)的值0，但由于现在是一维数组，所以dp[2 - weight[0]]就成了（物品1，下标1）的值15，由于value[0]也是15，所以dp[2]得到了30

此时dp[2]就已经是30了，意味着物品0，被放入了两次，所以不能正序遍历。

为什么倒序遍历，就可以保证物品只放入一次呢？

倒序就是先算dp[2]

dp[2] = max(dp[2 - weight[0]] + value[0], dp[2]) = 15 （dp数组已经都初始化为0，这里的dp[2]为0，且dp[2-1]也为0）

dp[1] = max(dp[1 - weight[0]] + value[0], dp[1]) = 15

所以从后往前循环，每次取得状态不会和之前取得状态重合，这样每种物品就只取一次了。

那么问题又来了，为什么二维dp数组遍历的时候不用倒序呢？

因为对于二维dp，dp[i][j]都是通过上一层即dp[i - 1][j]计算而来，本层的dp[i][j]并不会被覆盖！（看刚刚的table例子）

（如何这里读不懂，大家就要动手试一试了，空想还是不靠谱的，实践出真知！）

再来看看两个嵌套for循环的顺序，代码中是先遍历物品嵌套遍历背包容量，那可不可以先遍历背包容量嵌套遍历物品呢？

不可以！

因为一维dp的写法，背包容量一定是要倒序遍历（原因上面已经讲了），如果遍历背包容量放在上一层，那么每个dp[j]就只会放入一个物品，即：背包里只放入了一个物品。

所以一维dp数组的背包在遍历顺序上和二维其实是有很大差异的！，这一点大家一定要注意。

携带研究材料（第六期模拟笔试）

题目描述

小明是一位科学家，他需要参加一场重要的国际科学大会，以展示自己的最新研究成果。他需要带一些研究材料，但是他的行李箱空间有限。这些研究材料包括实验设备、文献资料和实验样本等等，它们各自占据不同的空间，并且具有不同的价值。

小明的行李空间为 N，问小明应该如何抉择，才能携带最大价值的研究材料，每种研究材料只能选择一次，并且只有选与不选两种选择，不能进行切割。

输入描述

第一行包含两个正整数，第一个整数 M 代表研究材料的种类，第二个正整数 N，代表小明的行李空间。

第二行包含 M 个正整数，代表每种研究材料的所占空间。

第三行包含 M 个正整数，代表每种研究材料的价值。

输出描述

输出一个整数，代表小明能够携带的研究材料的最大价值。

输入示例

6 1
2 2 3 1 5 2
2 3 1 5 4 3

输出示例

5

提示信息

小明能够携带 6 种研究材料，但是行李空间只有 1，而占用空间为 1 的研究材料价值为 5，所以最终答案输出 5。

数据范围：
1 <= N <= 5000
1 <= M <= 5000
研究材料占用空间和价值都小于等于 1000

动态规划思路

dp数组创建，创建个二维背包（简单直观）

dp下标与含义：dp[i][j]表示物品i以及dp容量j时的背包价值

递推公式分成放物品i与不放物品i两种情况

如果不放物品i,则dp[i][j] = dp[i - 1][j]

如果放物品i， 则dp[i][j] = dp[i - 1][j - weight] + val[i]

递推公式：dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + val[i])

dp初始化，dp[i][0]全部为0，遍历dp[0][j]，如果j大于等于weight[0]则赋值为val[0]

遍历顺序，行遍历对物品，列遍历对背包容量

二维dp动态规划代码

class solution():
    def __init__(self):
        self.res = 0
    
    def calMaxVal(self, n: int, capacity: int, weight: list, val: list) -> int:
        # 注意背包容量从0开始到capacity(闭区间)，所以个数为capacity+1
        dp = [[0] * (capacity + 1) for j in range(n)]

        # 初始化第一个物品
        for j in range(weight[0], capacity + 1):
            dp[0][j] = val[0]

        for i in range(1, n):
            for j in range(capacity + 1):
                # 如果j装不下，直接继续上一物品此时的背包状态
                if j < weight[i]:
                    dp[i][j] = dp[i - 1][j]
                # 如果j能装下
                else:
                    dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + val[i])
        
        # print(dp)
        return dp[n - 1][capacity]

n, capacity = map(int, input().split(" "))
weight = list(map(int, input().split(" ")))
val = list(map(int, input().split(" ")))

s = solution()
res = s.calMaxVal(n, capacity, weight, val)
print(res)

一维dp动态规划代码

class solution2():
    def calMaxVal(self, n: int, capacity: int, weight: list, val: list) -> int:
        # dp用一维就行，长度是capacity
        dp = [0] * (capacity + 1)
        
        # 行遍历与列遍历
        # 行遍历物品
        for i in range(n):
            # 一维dp要倒序遍历，为了避免 数据污染。
            for j in range(capacity, weight[i] - 1, -1):
                if j >= weight[i]:
                    dp[j] = max(dp[j], dp[j - weight[i]] + val[i])

        return dp[capacity]

n, capacity = map(int, input().split(" "))
weight = list(map(int, input().split(" ")))
val = list(map(int, input().split(" ")))

s2 = solution2()
res2 = s2.calMaxVal(n, capacity, weight, val)
print(res2)

416. 分割等和子集

https://leetcode.cn/problems/partition-equal-subset-sum/

给你一个 只包含正整数 的 非空 数组 nums 。请你判断是否可以将这个数组分割成两个子集，使得两个子集的元素和相等。

示例 1：

输入：nums = [1,5,11,5]
输出：true
解释：数组可以分割成 [1, 5, 5] 和 [11] 。

示例 2：

输入：nums = [1,2,3,5]
输出：false
解释：数组不能分割成两个元素和相等的子集。

提示：

• 1 <= nums.length <= 200
• 1 <= nums[i] <= 100

动态划分思路

将这个问题抽象成动态规划问题，target看作背包容量，而nums[i]既是重量也是价值

问题转换：一共n个物品，每个物品选择一个，背包容量为target，能否让总价值也为target（即dp[target] == target） ，其中，target为列表和的一半

1. dp数组下标与含义：创建一维数组，下标i是weight（也是数字本身），dp[i]值表示当前背包总价值；dp长度： 背包容量为target + 1即可

2. 递推公式：倒序遍历，并且dp[j]大于nums[i]，此时dp[j] = max(dp[j], dp[j - nums[i]]+nums[i])

3. 初始化：全部为零

4. 遍历顺序：物品（nums[i]）顺序遍历；而对于每个背包容量从target倒序遍历，一直到nums[i]（闭区间）

5. 举例

6. nums[1, 5, 11, 5]

7. target = 11

8. dp[0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]

10. i = 0, nums[0]=1, j = 11

11. dp[11] = max[dp[11], dp[11 - 1] + 1] = 1

12. dp[10] = max[dp[10], dp[10 - 1] + 1] = 1

13. …

14. dp[1] = max[dp[1], dp[1 - 1] + 1] = 1

15. dp[0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1]

17. i = 1, nums[1]=5, j = 11

18. dp[11] = max[dp[11], dp[11 - 5] + 5] = 6

19. dp[10] = max[dp[10], dp[10 - 5] + 5] = 6

20. …

21. dp[5] = max[dp[5], dp[5 - 5] + 5] = 6

22. [0, 1, 1, 1, 1, 5, 6, 6, 6, 6, 6, 6]

24. i = 2, nums[2]=11, j = 11

25. dp[11] = max[dp[11], dp[11 - 11] + 11] = 11

26. [0, 1, 1, 1, 1, 5, 6, 6, 6, 6, 6, 11]

28. i = 3, nums[3]=5, j=11

29. dp[11] = max[dp[11], dp[11 - 5] + 5] = max(11, dp[6] + 5) = 11

30. dp[10] = max[dp[10], dp[10 - 5] + 5] = max(6, dp[5] + 5) = 10

31. dp[9] = max[dp[9], dp[9 - 5] + 5] = max(6, dp[4] + 5) = 6

32. …

33. [0, 1, 1, 1, 1, 5, 6, 6, 6, 6, 10, 11]

动态规划代码

class Solution:

  def canPartition(self, nums: List[int]) -> bool:
        self.sumOfnums = sum(nums)
        self.LOfnums = len(nums)
        self.nums = nums
        if self.sumOfnums % 2 != 0 :
            return False
        self.target = self.sumOfnums // 2
        # 动态规划
        dp = [0] * (self.target + 1)

        L = len(nums)
        for i in range(L):
            for j in range(self.target, nums[i] - 1, -1):
                dp[j] = max(dp[j], dp[j - nums[i]]+nums[i])
        
        if dp[self.target] == self.target:
            return True
        return False

递归思路

本题目要求将数组分成两个子集，对于任意一个元素，要么在子集A，要么在子集B中

所以，如果暴力枚举出所有子集，判断两个子集和是否相等（直接判断当前子集和是否等于sum(nums)//2）

因为每个元素只有“被选中到子集A”和不被选择到子集A；而剩下的元素则可以看到一个子问题，可以考虑使用递归求解

定义 dfs(i,sum) 表示处理前 i 个元素后的总和为 sum，当前正在抉择第 i 个元素，判断能否凑成目标 target

第 i 个元素只有 “选或不选” 两种可能，状态转移 方程为：

$dfs(i,sum)=dfs(i+1,sum+nums[i]) \lor dfs(i+1,sum)$

递归边界： i == n表示处理完所有元素，返回失败；或者 sum=target 表示当前子集符合目标，返回成功。

递归入口： dfs(0,0)，表示从下标 0 开始搜索，目前总和为 0

注意，这里使用了@cache装饰器，避免重复搜索，降低时间复杂度。递归的参数只有两个，所以记忆化数组需要两维。

@cache 的作用

备忘录化机制：@cache 会自动为函数的参数组合缓存结果。例如，dfs 函数的参数是 (index, currentSum)，每次调用 dfs(index, currentSum) 时，如果这个参数组合之前已经计算过，结果会直接从缓存中取出，而不会重新执行函数体。

为什么需要它？ 在递归过程中，可能会多次遇到相同的状态。例如：

假设数组是 [1, 2, 3]，在不同分支中，可能会多次调用 dfs(2, 3)（即在索引 2 时，当前和为 3）。

如果不缓存，这些重复的调用会独立计算，导致时间复杂度从 O(1) 或 O(2^n) 级别的子问题中浪费大量时间。

使用 @cache 后，这些重复状态只计算一次，后续直接返回结果。

效率提升：这个问题的原始递归复杂度是 O(2^n)，因为有 n 个元素，每个元素两个选择。但通过 @cache，函数会将重叠子问题（overlapping subproblems）缓存起来，实际时间复杂度会降低到接近 O(n * target)，这取决于数组的大小和目标和的大小。更高效，避免了不必要的递归调用。

递归代码

def canPartition(self, nums: List[int]) -> bool:
      self.sumOfnums = sum(nums)
      self.LOfnums = len(nums)
      self.nums = nums
      if self.sumOfnums % 2 != 0 :
          return False
      self.target = self.sumOfnums // 2

      @cache
      def dfs(index, currentSum):
          if currentSum == self.target:
              return True
          if index == self.LOfnums:
              return False
          # 每个数字都有选或不选两种情况
          return (dfs(index + 1, currentSum + nums[index]) or dfs(index + 1, currentSum))

      return dfs(0, 0)

额外题目

21. 合并两个有序链表

https://leetcode.cn/problems/merge-two-sorted-lists/

将两个升序链表合并为一个新的 升序 链表并返回。新链表是通过拼接给定的两个链表的所有节点组成的。

示例 1：

输入：l1 = [1,2,4], l2 = [1,3,4]
输出：[1,1,2,3,4,4]

示例 2：

输入：l1 = [], l2 = []
输出：[]

示例 3：

输入：l1 = [], l2 = [0]
输出：[0]

提示：

• 两个链表的节点数目范围是 [0, 50]
• -100 <= Node.val <= 100
• l1 和 l2 均按 非递减顺序 排列

思路

如果使用新空间head，如果list1和list2（指两个具体节点）不为空，则比较两者的值并将较小的值放在head里，并移动较小值所在的链表

最后再判断如果list1或list2不为空，则将list1或list2接到head里

链表代码

# Definition for singly-linked list.
# class ListNode:
#     def __init__(self, val=0, next=None):
#         self.val = val
#         self.next = next
class Solution:
    def mergeTwoLists(self, list1: Optional[ListNode], list2: Optional[ListNode]) -> Optional[ListNode]:
        # 双指针
        # 如果需要原地添加（不使用新空间的话，稍微麻烦一点儿）

        # 使用新空间
        head = ListNode()
        p = head

        while list1 and list2:
            if list1.val < list2.val:
                p.next = list1
                list1 = list1.next
            else:
                p.next = list2
                list2 = list2.next
            p = p.next

        if list1 is not None:
            p.next = list1
        else:
            p.next = list2
        return head.next

228. 汇总区间

https://leetcode.cn/problems/summary-ranges/

给定一个 无重复元素 的 有序 整数数组 nums 。

区间 [a,b] 是从 a 到 b（包含）的所有整数的集合。

返回 恰好覆盖数组中所有数字 的 最小有序 区间范围列表 。也就是说，nums 的每个元素都恰好被某个区间范围所覆盖，并且不存在属于某个区间但不属于 nums 的数字 x 。

列表中的每个区间范围 [a,b] 应该按如下格式输出：

• "a->b" ，如果 a != b
• "a" ，如果 a == b

示例 1：

输入：nums = [0,1,2,4,5,7]
输出：["0->2","4->5","7"]
解释：区间范围是：
[0,2] --> "0->2"
[4,5] --> "4->5"
[7,7] --> "7"

示例 2：

输入：nums = [0,2,3,4,6,8,9]
输出：["0","2->4","6","8->9"]
解释：区间范围是：
[0,0] --> "0"
[2,4] --> "2->4"
[6,6] --> "6"
[8,9] --> "8->9"

提示：

• 0 <= nums.length <= 20
• -231 <= nums[i] <= 231 - 1
• nums 中的所有值都 互不相同
• nums 按升序排列

思路

1. 从数组下标0开始向右遍历，如果相邻元素之间差值大于1，则找到了一个区间
2. 遍历过程中，slow指向区间起点，fast指向区间终点；当找到一个区间时，再分情况将字符串添加到res
   1. 先创建个temp=str(nums[slow])
   2. 如果nums[slow] != nums[fast]，则再将temp += “->” + str(nums[fast])

代码

class Solution:
    def summaryRanges(self, nums: List[int]) -> List[str]:
        # 用双指针
        # 先动快指针，若fast +1 != i则将slow~fast添加到结果
        # slow = 0
        # fast = 0
        # if len(nums) == 0:
        #     return []
        # # 复制一个值，填充结尾
        # nums.append(nums[-1])
        # L = len(nums)
        # if L == 1:
        #     return [str(nums[0])]

        # res = list()
        # def foo(slow, fast, res):
        #     if nums[slow] == nums[fast]:
        #         res.append(str(nums[slow]))
        #     else:
        #         res.append(str(nums[slow]) + "->" + str(nums[fast]) )

        # for i in range(1, L):
        #     if nums[i] != nums[fast] + 1:
        #         foo(slow, fast, res)
        #         slow = i
        #     fast = i
        res = list()
        i = 0 
        L = len(nums)
        while i < L:
            slow = i
            i += 1
            while i < L and nums[i] == nums[i - 1] + 1:
                i += 1
            fast = i - 1
            temp = str(nums[slow])
            if nums[slow] != nums[fast]:
                temp += "->" + str(nums[fast])
            res.append(temp)
        
        return res