LeetCodeCampsDay56图论part06
无向图&有向图变成无向树&有向树问题
108.冗余的边
题目描述
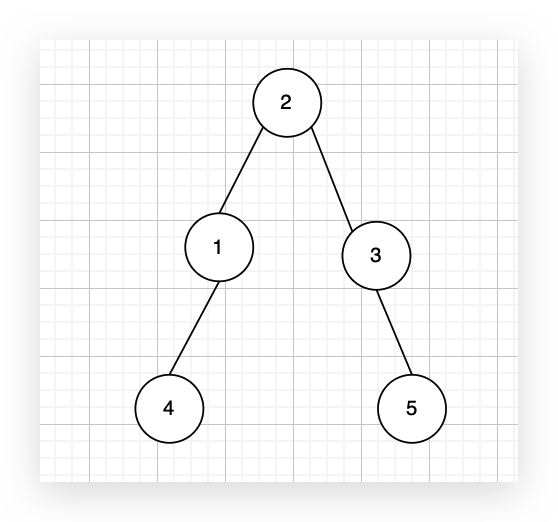
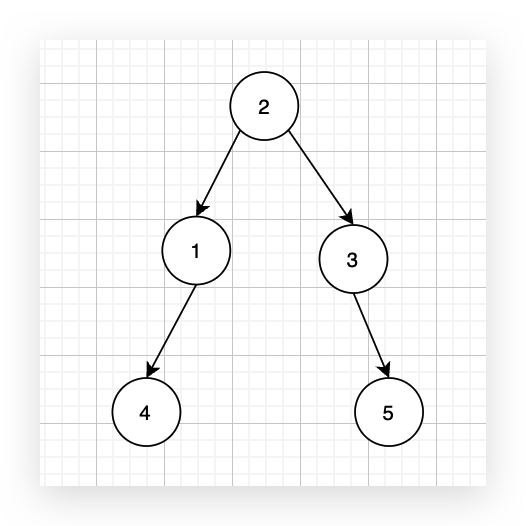
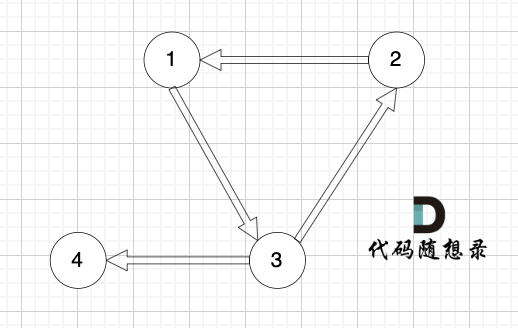
有一个图,它是一棵树,他是拥有 n 个节点(节点编号1到n)和 n - 1 条边的连通无环无向图,例如如图:
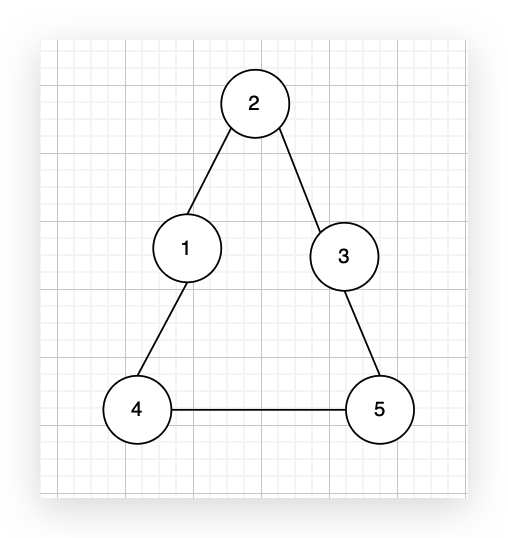
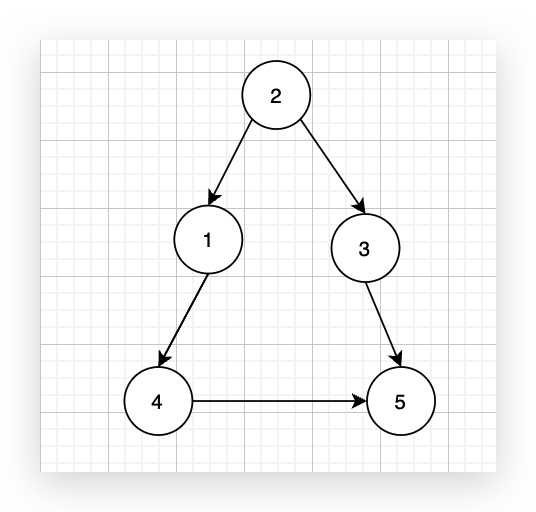
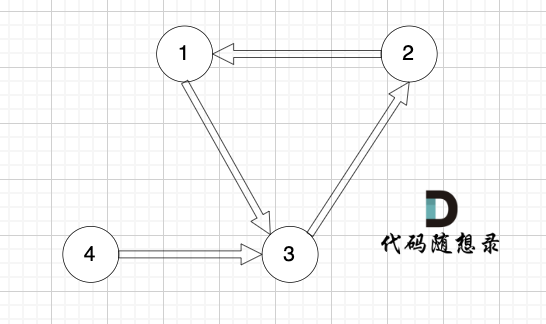
现在在这棵树上的基础上,添加一条边(依然是n个节点,但有n条边),使这个图变成了有环图,如图:
先请你找出冗余边,删除后,使该图可以重新变成一棵树。
输入描述
第一行包含一个整数 N,表示图的节点个数和边的个数。
后续 N 行,每行包含两个整数 s 和 t,表示图中 s 和 t 之间有一条边。
输出描述
输出一条可以删除的边。如果有多个答案,请删除标准输入中最后出现的那条边。
输入示例
输出示例
提示信息
图中的 1 2,2 3,1 3 等三条边在删除后都能使原图变为一棵合法的树。但是 1 3 由于是标准输出里最后出现的那条边,所以输出结果为 1 3
数据范围:
1 <= N <= 1000.
并查集思路
如何判断哪条边是多余的?
对输入的边进行遍历,如果这边的两个节点已经在并查集里了,则说明这边就是多余的,可以把这边添加到备选列表;否则,再添加到并查集中
并查集代码
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 class UnionFind : def __init__ (self, size ): self.parent = list (range (size + 1 )) def find (self, u ): if self.parent[u] != u: self.parent[u] = self.find(self.parent[u]) return self.parent[u] def join (self, u, v ): root_u = self.find(u) root_v = self.find(v) if root_u != root_v: self.parent[root_v] = root_u def isSame (self, u, v ): return self.find(u) == self.find(v) def main (): n = int (input ()) union = UnionFind(n) res = list () for _ in range (n): s, t = map (int , input ().split()) if union.isSame(s, t): print (s, t) break else : union.join(s, t) if __name__ == "__main__" : main()
扩展
题目要求 “请删除标准输入中最后出现的那条边” ,不少录友疑惑,这代码分明是遇到在同一个根的两个节点立刻就返回了,怎么就求出 最后出现的那条边 了呢。
有这种疑惑的录友是 认为发现一条冗余边后,后面还可能会有一条冗余边。
其实并不会。
题目是在 树的基础上 添加一条边,所以冗余边仅仅是一条。
到这一条可能靠前出现,可能靠后出现。
例如,题目输入示例:
输入示例
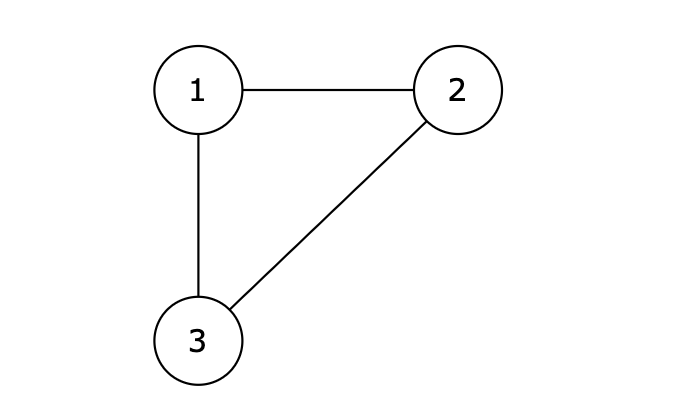
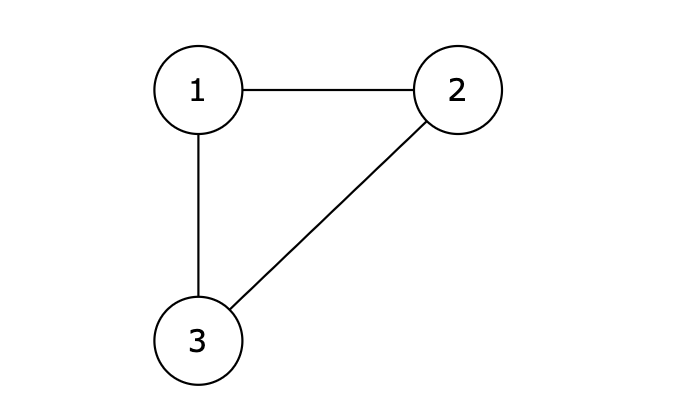
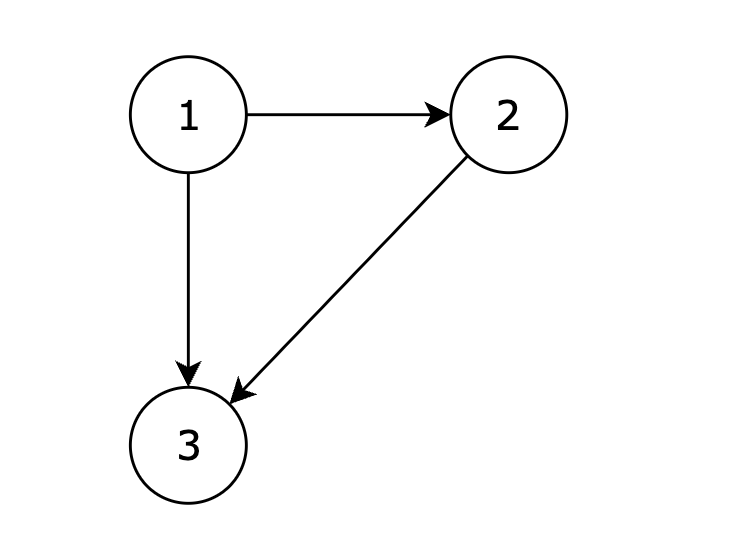
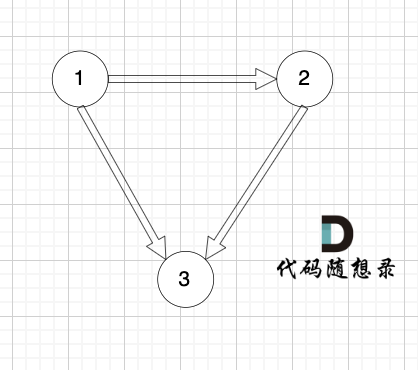
图:
输出示例
1 3
当我们从前向后遍历,优先让前面的边连上,最后判断冗余边就是 1 3。
如果我们从后向前便利,优先让后面的边连上,最后判断的冗余边就是 1 2。
题目要求“请删除标准输入中最后出现的那条边”,所以 1 3 这条边才是我们要求的
思路
如何判断哪条边是多余的?
对输入的边进行遍历,如果这边的两个节点已经在并查集里了,则说明这边就是多余的
可以把这边备选
代码
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 class UnionFind : def __init__ (self, size ): self.parent = list (range (size + 1 )) def find (self, u ): if self.parent[u] != u: self.parent[u] = self.find(self.parent[u]) return self.parent[u] def join (self, u, v ): root_u = self.find(u) root_v = self.find(v) if root_u != root_v: self.parent[root_v] = root_u def isSame (self, u, v ): return self.find(u) == self.find(v) def main (): n = int (input ()) union = UnionFind(n) res = list () for _ in range (n): s, t = map (int , input ().split()) if union.isSame(s, t): print (s, t) break else : union.join(s, t) if __name__ == "__main__" : main()
109.冗余的边II
题目描述
有一种有向树,该树只有一个根节点,所有其他节点都是该根节点的后继。该树除了根节点之外的每一个节点都有且只有一个父节点,而根节点没有父节点。有向树拥有 n 个节点和 n - 1 条边。如图:
现在有一个有向图,有向图是在有向树中的两个没有直接链接的节点中间添加一条有向边。如图:
输入一个有向图,该图由一个有着 n 个节点(节点编号 从 1 到 n),n 条边,请返回一条可以删除的边,使得删除该条边之后该有向图可以被当作一颗有向树。
输入描述
第一行输入一个整数 N,表示有向图中节点和边的个数。
后续 N 行,每行输入两个整数 s 和 t,代表这是 s 节点连接并指向 t 节点的单向边
输出描述
输出一条可以删除的边,若有多条边可以删除,请输出标准输入中最后出现的一条边。
输入示例
输出示例
提示信息
在删除 2 3 后有向图可以变为一棵合法的有向树,所以输出 2 3
数据范围:
1 <= N <= 1000.
思路
本题与 108.冗余连接 类似,但本题是一个有向图,有向图相对要复杂一些。
本题的本质是 :有一个有向图,是由一颗有向树 + 一条有向边组成的 (所以此时这个图就不能称之为有向树),现在让我们找到那条边 把这条边删了,让这个图恢复为有向树。
还有“若有多条边可以删除,请输出标准输入中最后出现的一条边 ”,这说明在两条边都可以删除的情况下,要删顺序靠后的边!
我们来想一下 有向树的性质,如果是有向树的话,只有根节点入度为0,其他节点入度都为1(因为该树除了根节点之外的每一个节点都有且只有一个父节点,而根节点没有父节点)。
所以情况一:如果我们找到入度为2的点,那么删一条指向该节点的边就行了。
如图:
找到了节点3 的入度为2,删 1 -> 3 或者 2 -> 3 。选择删顺序靠后便可。
但 入度为2 还有一种情况,情况二,只能删特定的一条边,如图:
节点3 的入度为 2,但在删除边的时候,只能删 这条边(节点1 -> 节点3),如果删这条边(节点4 -> 节点3),那么删后本图也不是有向树了(因为找不到根节点)。
综上,如果发现入度为2的节点,我们需要判断 删除哪一条边,删除后本图能成为有向树。如果是删哪个都可以,优先删顺序靠后的边。
情况三: 如果没有入度为2的点,说明 图中有环了(注意是有向环)。
如图:
对于情况三,删掉构成环的边就可以了
代码
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 class UnionFind : def __init__ (self, size ): self.parent = list (range (size + 1 )) def find (self, u ): if self.parent[u] != u: self.parent[u] = self.find(self.parent[u]) return self.parent[u] def join (self, u, v ): root_u = self.find(u) root_v = self.find(v) if root_u != root_v: self.parent[root_v] = root_u def isSame (self, u, v ): return self.find(u) == self.find(v) def isLegal (graph, edge:list ) -> bool : s, t = edge union = UnionFind(len (graph)) for u, v in graph: if u == s and v == t: continue if union.isSame(u, v): return False else : union.join(u, v) return True def main (): n = int (input ()) indegree = [0 ] * (n + 1 ) graph = list () for _ in range (n): s, t = map (int , input ().split()) graph.append([s, t]) indegree[t] += 1 res = list () for s, t in graph: if indegree[t] == 2 : res.append([s, t]) if len (res) > 0 : if isLegal(graph, res[-1 ]): u, v = res[-1 ] print (u, v) else : u, v = res[-2 ] print (u, v) else : union = UnionFind(n) for u, v in graph: if union.isSame(u, v): print (u, v) return else : union.join(u, v) if __name__ == "__main__" : main()