LeetCodeCampsDay58图论part08

拓扑排序与dijkstra初识

117.软件构建

题目描述

某个大型软件项目的构建系统拥有 N 个文件，文件编号从 0 到 N - 1，在这些文件中，某些文件依赖于其他文件的内容，这意味着如果文件 A 依赖于文件 B，则必须在处理文件 A 之前处理文件 B （0 <= A, B <= N - 1）。请编写一个算法，用于确定文件处理的顺序。

输入描述

第一行输入两个正整数 N, M。表示 N 个文件之间拥有 M 条依赖关系。

后续 M 行，每行两个正整数 S 和 T，表示 T 文件依赖于 S 文件。

输出描述

输出共一行，如果能处理成功，则输出文件顺序，用空格隔开。

如果不能成功处理（相互依赖），则输出 -1。

输入示例

1
2
3
4
5
5 4
0 1
0 2
1 3
2 4

输出示例

1
0 1 2 3 4

提示信息

文件依赖关系如下：

img

所以，文件处理的顺序除了示例中的顺序，还存在

0 2 4 1 3

0 2 1 3 4

等等合法的顺序。

数据范围：

0 <= N <= 10 ^ 5

1 <= M <= 10 ^ 9

每行末尾无空格

拓扑排序思路

拓扑排序指的是一种 解决问题的大体思路， 而具体算法，可能是广搜也可能是深搜。

大家可能发现 各式各样的解法，纠结哪个是拓扑排序？

其实只要能在把 有向无环图 进行线性排序 的算法 都可以叫做 拓扑排序。

实现拓扑排序的算法有两种：卡恩算法（BFS）和DFS

卡恩1962年提出这种解决拓扑排序的思路

一般来说我们只需要掌握 BFS （广度优先搜索）就可以了，清晰易懂，如果还想多了解一些，可以再去学一下 DFS 的思路，但 DFS 不是本篇重点。

接下来我们来讲解BFS的实现思路。

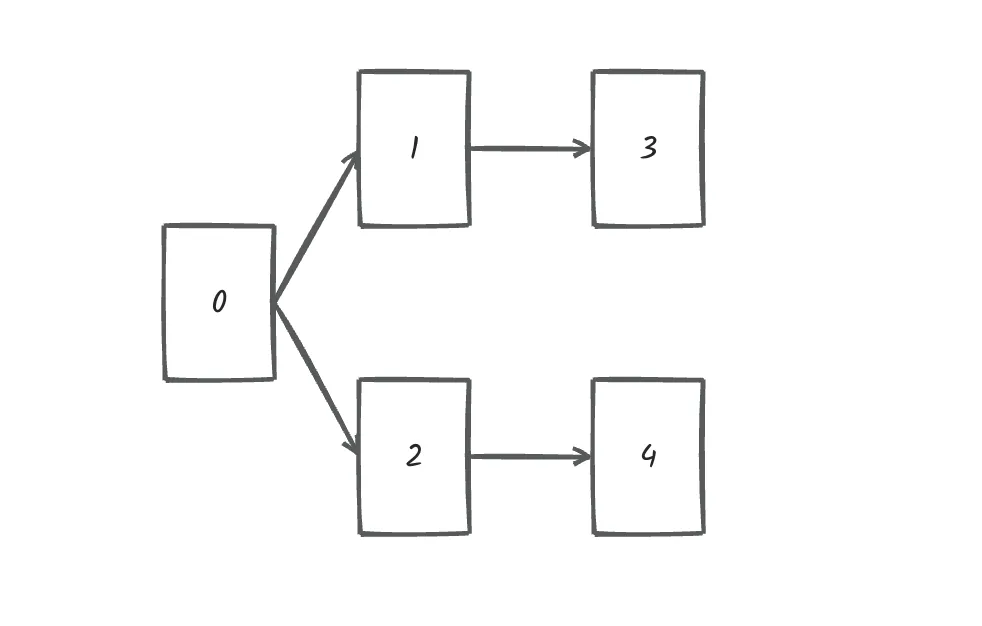
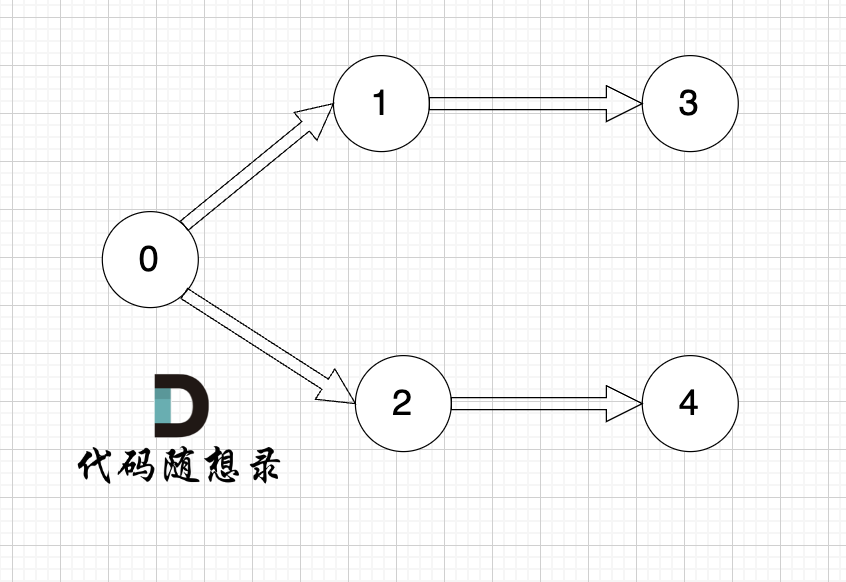
以题目中示例为例如图：

img

img

做拓扑排序的话，如果肉眼去找开头的节点，一定能找到 节点0 吧，都知道要从节点0 开始。

但为什么我们能找到 节点0呢，因为我们肉眼看着 这个图就是从 节点0出发的。

作为出发节点，它有什么特征？

你看节点0 的入度 为0 出度为2， 也就是 没有边指向它，而它有两条边是指出去的。

节点的入度表示 有多少条边指向它，节点的出度表示有多少条边 从该节点出发。

所以当我们做拓扑排序的时候，应该优先找 入度为 0 的节点，只有入度为0，它才是出发节点。 理解以上内容很重要！

接下来我给出 拓扑排序的过程，其实就两步：

  1. 找到入度为0 的节点，加入结果集
  2. 将该节点从图中移除

循环以上两步，直到 所有节点都在图中被移除了。

结果集的顺序，就是我们想要的拓扑排序顺序 （结果集里顺序可能不唯一）

模拟过程

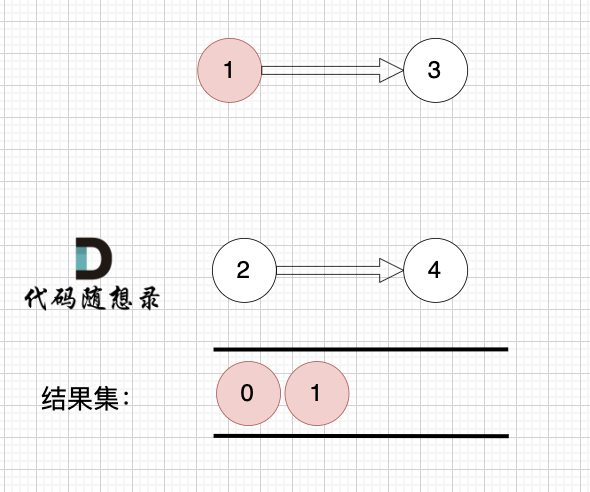
用本题的示例来模拟这一过程：

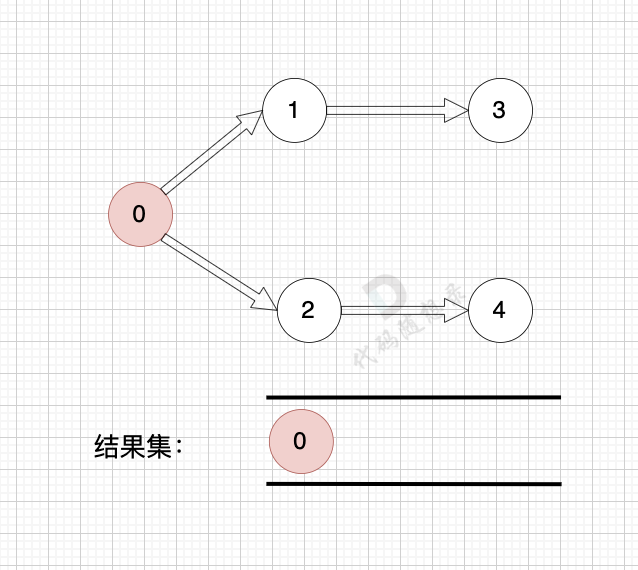
1、找到入度为0 的节点，加入结果集

img

img

2、将该节点从图中移除

img

img

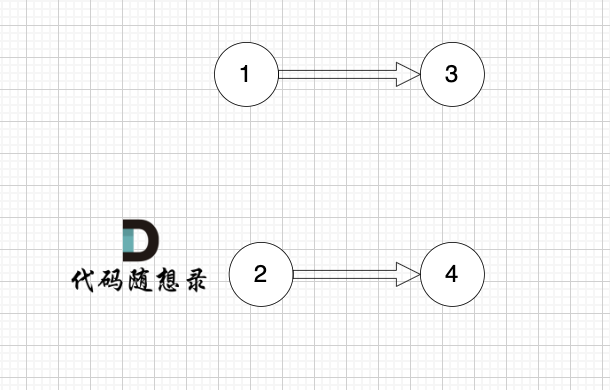
1、找到入度为0 的节点，加入结果集

img

img

这里大家会发现，节点1 和 节点2 入度都为0， 选哪个呢？

选哪个都行，所以这也是为什么拓扑排序的结果是不唯一的。

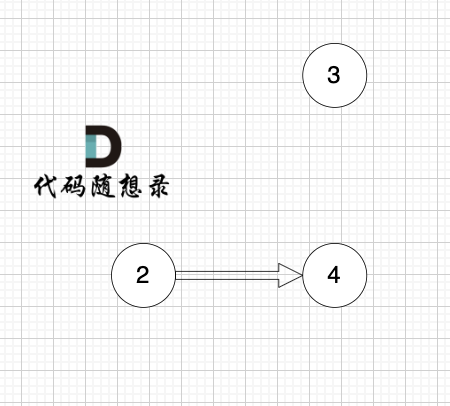
2、将该节点从图中移除

img

img

1、找到入度为0 的节点，加入结果集

img

img

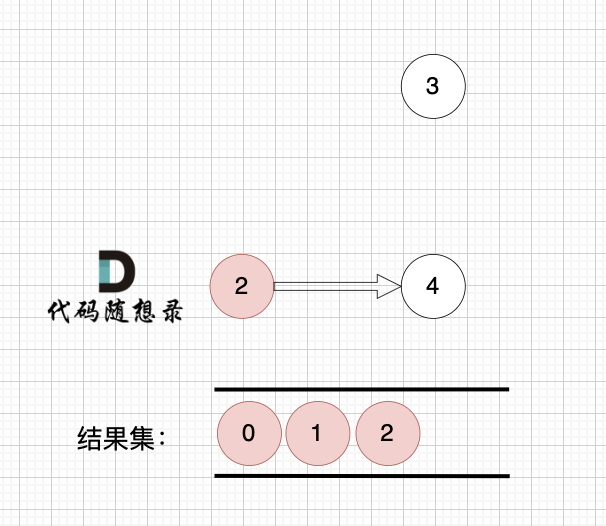
节点2 和 节点3 入度都为0，选哪个都行，这里选节点2

2、将该节点从图中移除

img

img

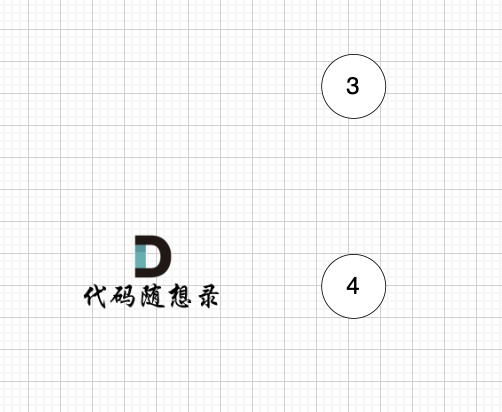
后面的过程一样的，节点3 和 节点4，入度都为0，选哪个都行。

最后结果集为： 0 1 2 3 4 。当然结果不唯一的。

判断有环

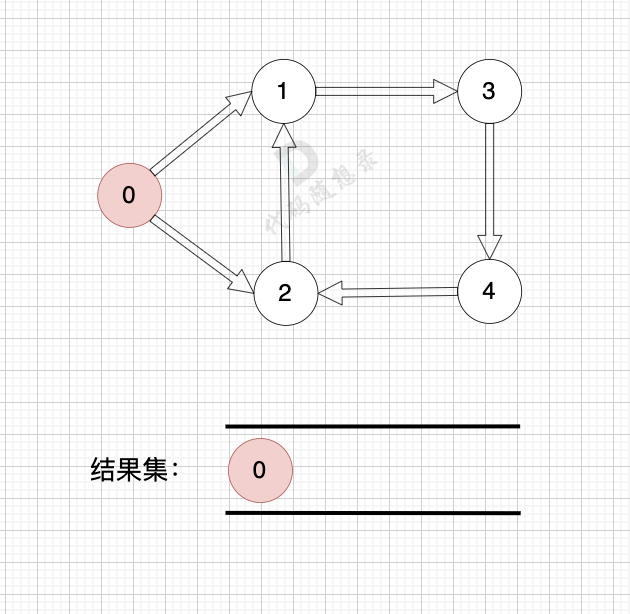
如果有 有向环怎么办呢？例如这个图：

img

img

这个图，我们只能将入度为0 的节点0 接入结果集。

之后，节点1、2、3、4 形成了环，找不到入度为0 的节点了，所以此时结果集里只有一个元素。

那么如果我们发现结果集元素个数 不等于 图中节点个数，我们就可以认定图中一定有 有向环！

这也是拓扑排序判断有向环的方法。

通过以上过程的模拟大家会发现这个拓扑排序好像不难，还有点简单

小技巧

  1. 构建一个字典里是列表的结构

如graph = {1:[], 2:[]}

1
2
from collections import defaultdict
graph = defaultdict(list)
  1. 将set/list里的元素输出成str

比如a = [1, 2, 3, 4]

如果直接print(a)会得到[1, 2, 3, 4]

如果要输出1, 2, 3, 4，可以使用下面的代码

1
print(" ".join(map(str, a)))
  1. 对列表进行带条件的初始化
1
DgreeZero = deque([i for i in range(n) if inDegree[i] == 0])

从而可以替换下面几行代码

1
2
3
4
5
from collections import deque
  DegreeZero = deque()
  for i in range(n):
      if inDegree[i] == 0:
          DegreeZero.append(i)

拓扑排序代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
def main():
    n, m = map(int, input().split())

    inDegree = [0] * (n)
		
    # from collections import defaultdict
    # graph = defaultdict(list) # 可以构建一个字典里是列表的结构
    graph = [[] for _ in range(n)]

    # edges = list()

    for _ in range(m):
        s, t = map(int, input().split())
        inDegree[t] += 1     
        graph[s].append(t)  
    
		
    # 将入度为0的节点添加到队列里，后面准备使用广度优先搜索对这些节点遍历 
    from collections import deque
    DegreeZero = deque()
    for i in range(n):
        if inDegree[i] == 0:
            DegreeZero.append(i)
            
    # 上面四行代码可以简化为
    # DgreeZero = deque([i for i in range(n) if inDegree[i] == 0])

    res = list()
    # 从入度为0的节点开始
    while DegreeZero:
        node = DegreeZero.popleft()
        res.append(str(node))
				
        # 将入度为0节点的终点节点入度减一
        for i in graph[node]:
            inDegree[i] -= 1
            # 如果入度为0了，也加入到队列中
            if inDegree[i] == 0:
                DegreeZero.append(i)

    # 判断是否有环，如果res的长度不等于图中节点个数n则有环
    if len(res) != n:
        print(-1)
        return
    
    print(" ".join(res))
    
    # 技巧二，使用map将字典里的数字变成字符串
    # print(" ".join(map(str, res)))

if __name__ == "__main__":
    main()

47.参加科学大会（第六期模拟笔试）

题目描述

小明是一位科学家，他需要参加一场重要的国际科学大会，以展示自己的最新研究成果。

小明的起点是第一个车站，终点是最后一个车站。然而，途中的各个车站之间的道路状况、交通拥堵程度以及可能的自然因素（如天气变化）等不同，这些因素都会影响每条路径的通行时间。

小明希望能选择一条花费时间最少的路线，以确保他能够尽快到达目的地。

输入描述

第一行包含两个正整数，第一个正整数 N 表示一共有 N 个公共汽车站，第二个正整数 M 表示有 M 条公路。

接下来为 M 行，每行包括三个整数，S、E 和 V，代表了从 S 车站可以单向直达 E 车站，并且需要花费 V 单位的时间。

输出描述

输出一个整数，代表小明从起点到终点所花费的最小时间。

输入示例

1
2
3
4
5
6
7
8
9
10
7 9
1 2 1
1 3 4
2 3 2
2 4 5
3 4 2
4 5 3
2 6 4
5 7 4
6 7 9

输出示例

1
12

提示信息

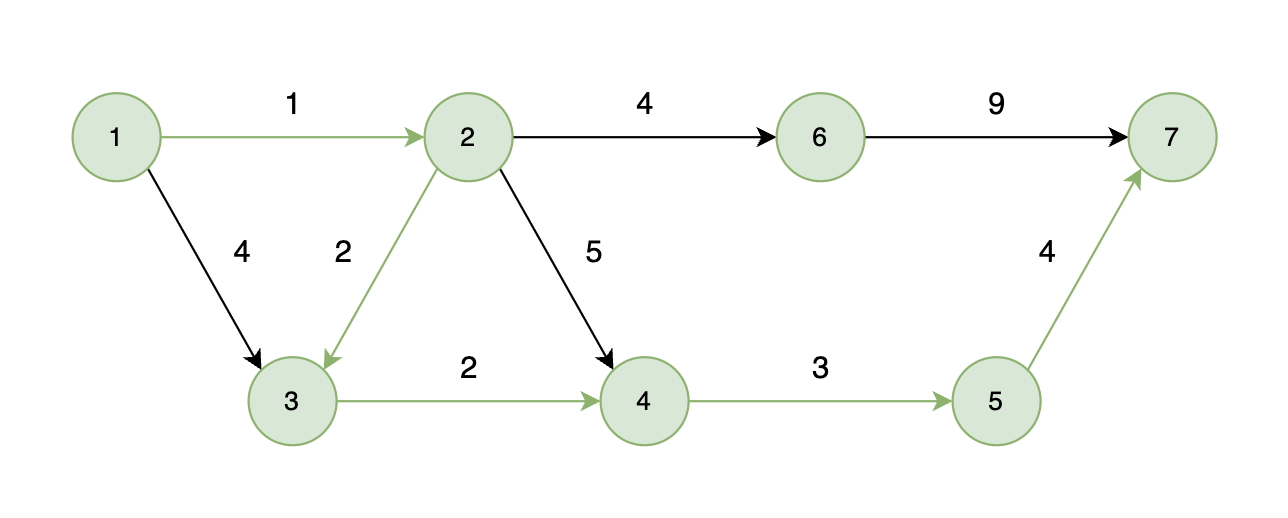
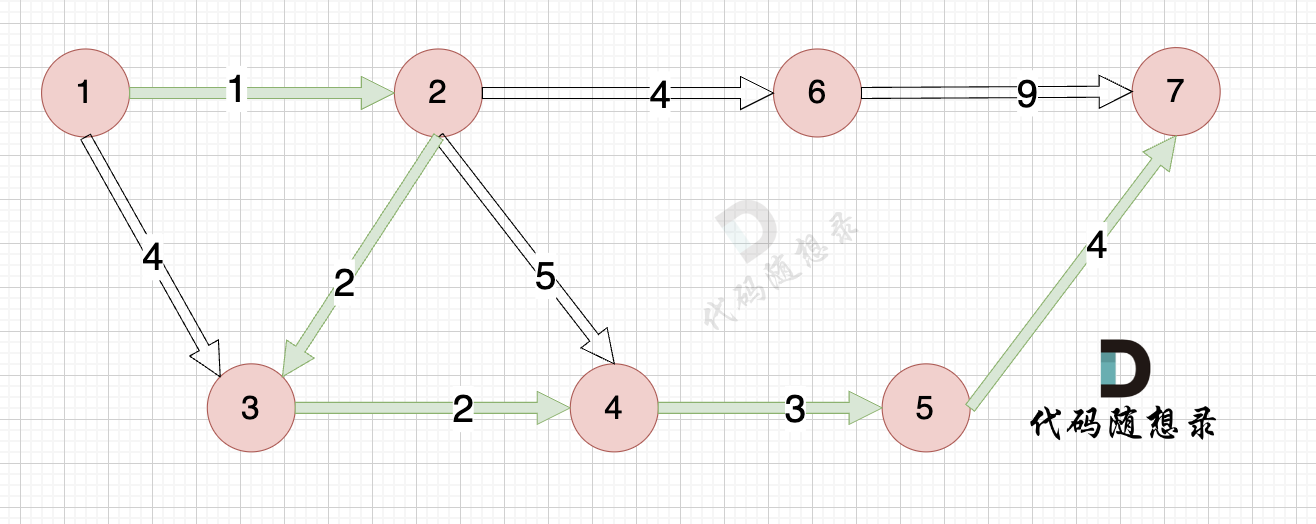
能够到达的情况：

如下图所示，起始车站为 1 号车站，终点车站为 7 号车站，绿色路线为最短的路线，路线总长度为 12，则输出 12。

img

**
**

不能到达的情况：

如下图所示，当从起始车站不能到达终点车站时，则输出 -1。

img

数据范围：

1 <= N <= 500;
1 <= M <= 5000;

dijkstra思路

模拟过程

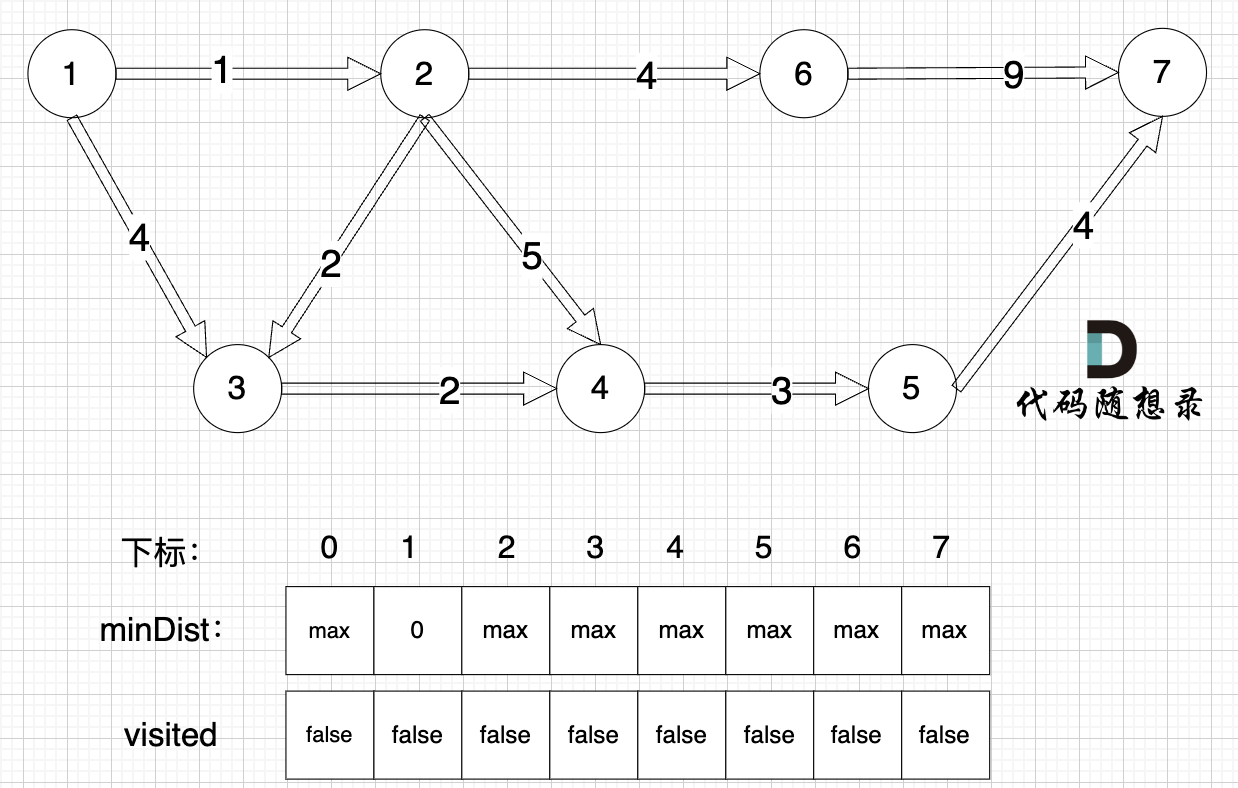
0、初始化

minDist数组数值初始化为int最大值。

这里在强点一下 minDist数组的含义：记录所有节点到源点的最短路径，那么初始化的时候就应该初始为最大值，这样才能在后续出现最短路径的时候及时更新。

img

img

（图中，max 表示默认值，节点0 不做处理，统一从下标1 开始计算，这样下标和节点数值统一， 方便大家理解，避免搞混）

源点（节点1） 到自己的距离为0，所以 minDist[1] = 0

此时所有节点都没有被访问过，所以 visited数组都为0

以下为dijkstra 三部曲

1、选源点到哪个节点近且该节点未被访问过

源点距离源点最近，距离为0，且未被访问。

2、该最近节点被标记访问过

标记源点访问过

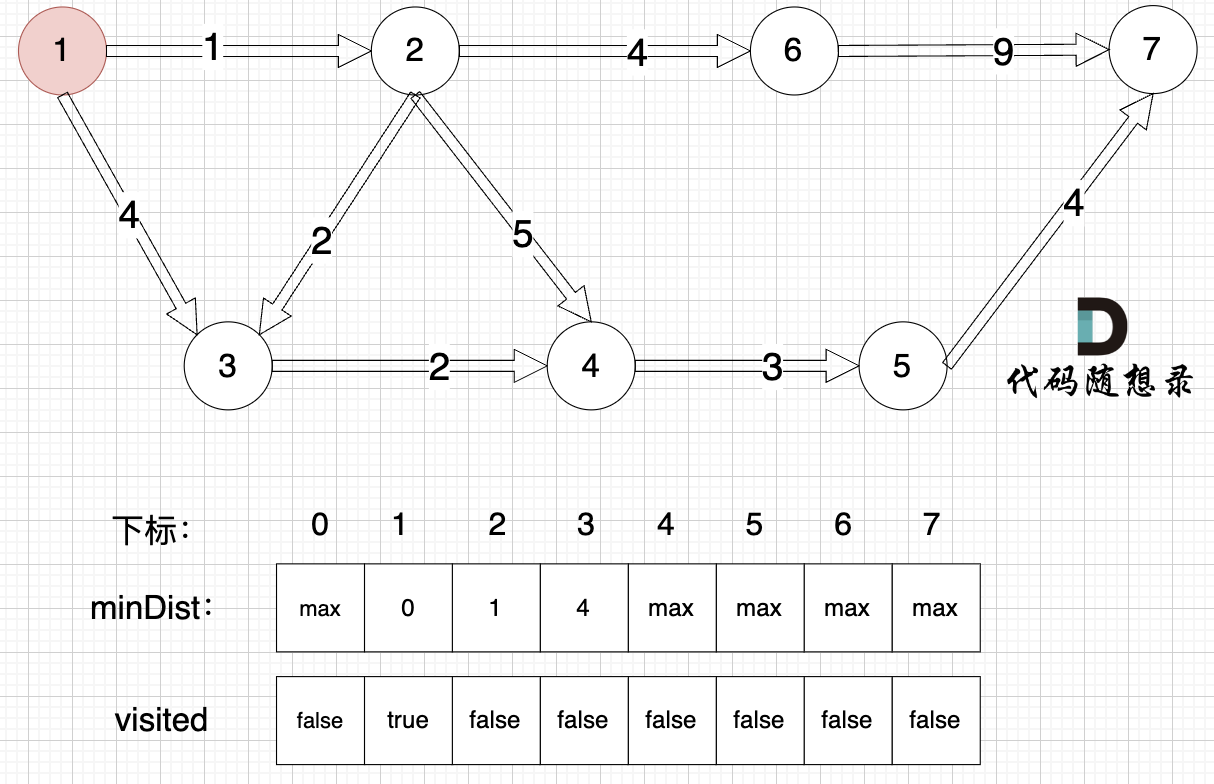
3、更新非访问节点到源点的距离（即更新minDist数组） ，如图：

img

img

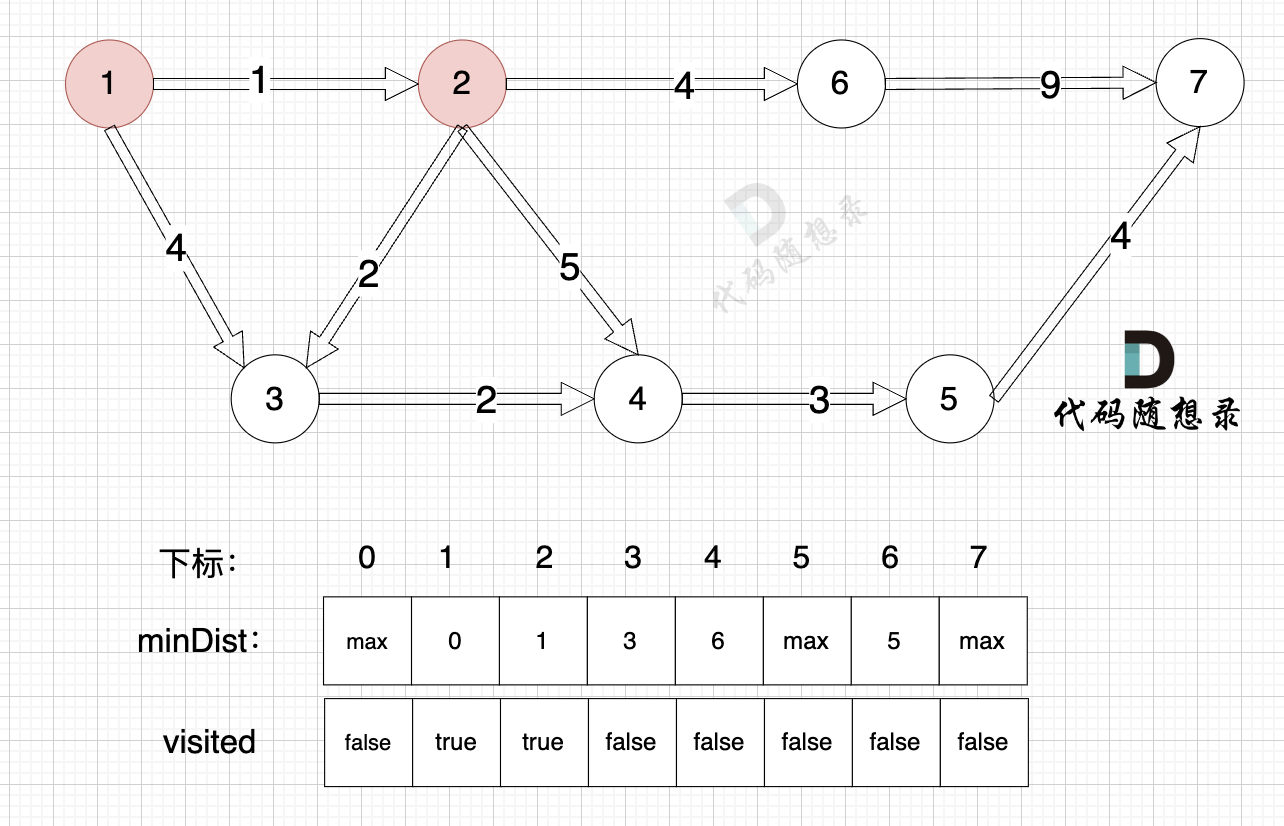
更新 minDist数组，即：源点（节点1） 到 节点2 和 节点3的距离。

  • 源点到节点2的最短距离为1，小于原minDist[2]的数值max，更新minDist[2] = 1
  • 源点到节点3的最短距离为4，小于原minDist[3]的数值max，更新minDist[3] = 4

可能有录友问：为啥和 minDist[2] 比较？

再强调一下 minDist[2] 的含义，它表示源点到节点2的最短距离，那么目前我们得到了 源点到节点2的最短距离为1，小于默认值max，所以更新。 minDist[3]的更新同理

1、选源点到哪个节点近且该节点未被访问过

未访问过的节点中，源点到节点2距离最近，选节点2

2、该最近节点被标记访问过

节点2被标记访问过

3、更新非访问节点到源点的距离（即更新minDist数组） ，如图：

img

img

更新 minDist数组，即：源点（节点1） 到 节点6 、 节点3 和 节点4的距离。

为什么更新这些节点呢？ 怎么不更新其他节点呢？

因为 源点（节点1）通过 已经计算过的节点（节点2） 可以链接到的节点 有 节点3，节点4和节点6.

更新 minDist数组：

  • 源点到节点6的最短距离为5，小于原minDist[6]的数值max，更新minDist[6] = 5
  • 源点到节点3的最短距离为3，小于原minDist[3]的数值4，更新minDist[3] = 3
  • 源点到节点4的最短距离为6，小于原minDist[4]的数值max，更新minDist[4] = 6

1、选源点到哪个节点近且该节点未被访问过

未访问过的节点中，源点距离哪些节点最近，怎么算的？

其实就是看 minDist数组里的数值，minDist 记录了 源点到所有节点的最近距离，结合visited数组筛选出未访问的节点就好。

从 上面的图，或者 从minDist数组中，我们都能看出 未访问过的节点中，源点（节点1）到节点3距离最近。

2、该最近节点被标记访问过

节点3被标记访问过

3、更新非访问节点到源点的距离（即更新minDist数组） ，如图：

img

img

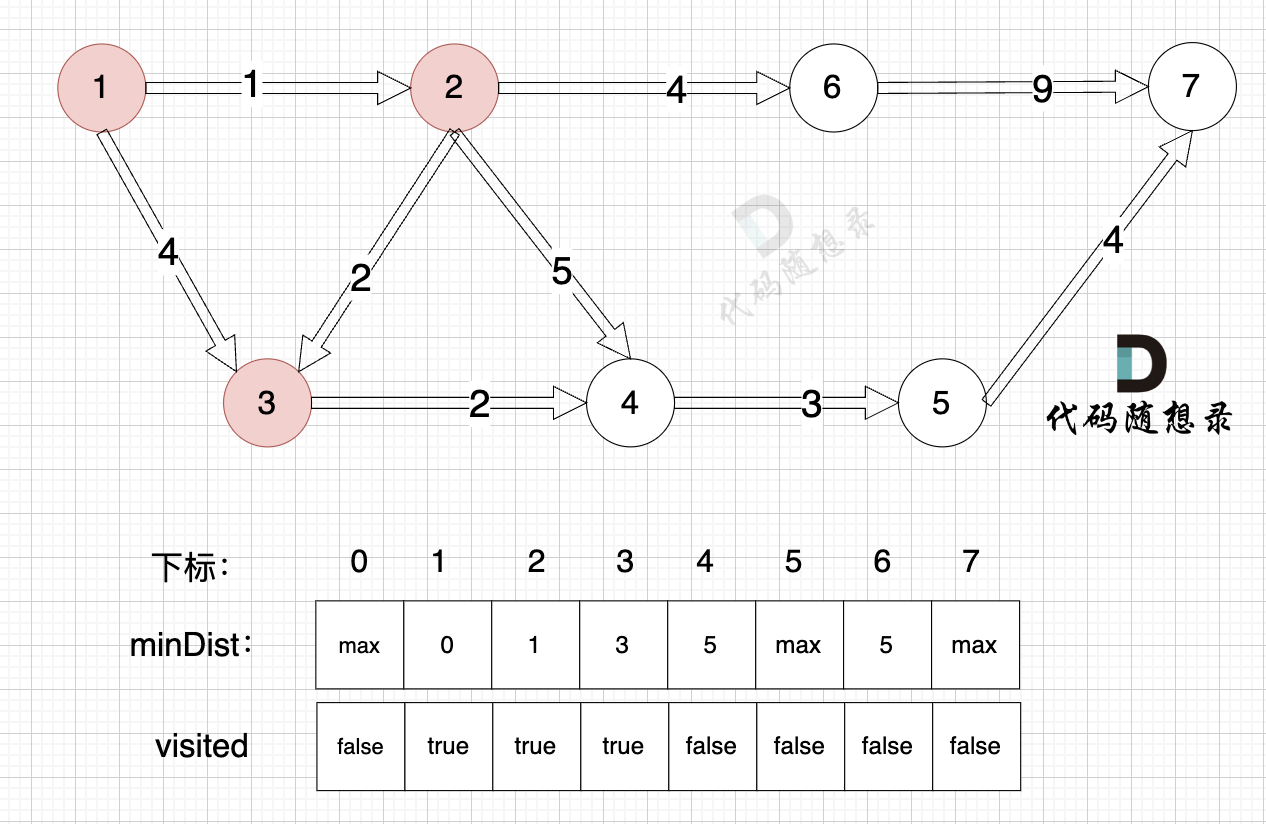
由于节点3的加入，那么源点可以有新的路径链接到节点4 所以更新minDist数组：

更新 minDist数组：

  • 源点到节点4的最短距离为5，小于原minDist[4]的数值6，更新minDist[4] = 5

1、选源点到哪个节点近且该节点未被访问过

距离源点最近且没有被访问过的节点，有节点4 和 节点6，距离源点距离都是 5 （minDist[4] = 5，minDist[6] = 5） ，选哪个节点都可以。

2、该最近节点被标记访问过

节点4被标记访问过

3、更新非访问节点到源点的距离（即更新minDist数组） ，如图：

img

img

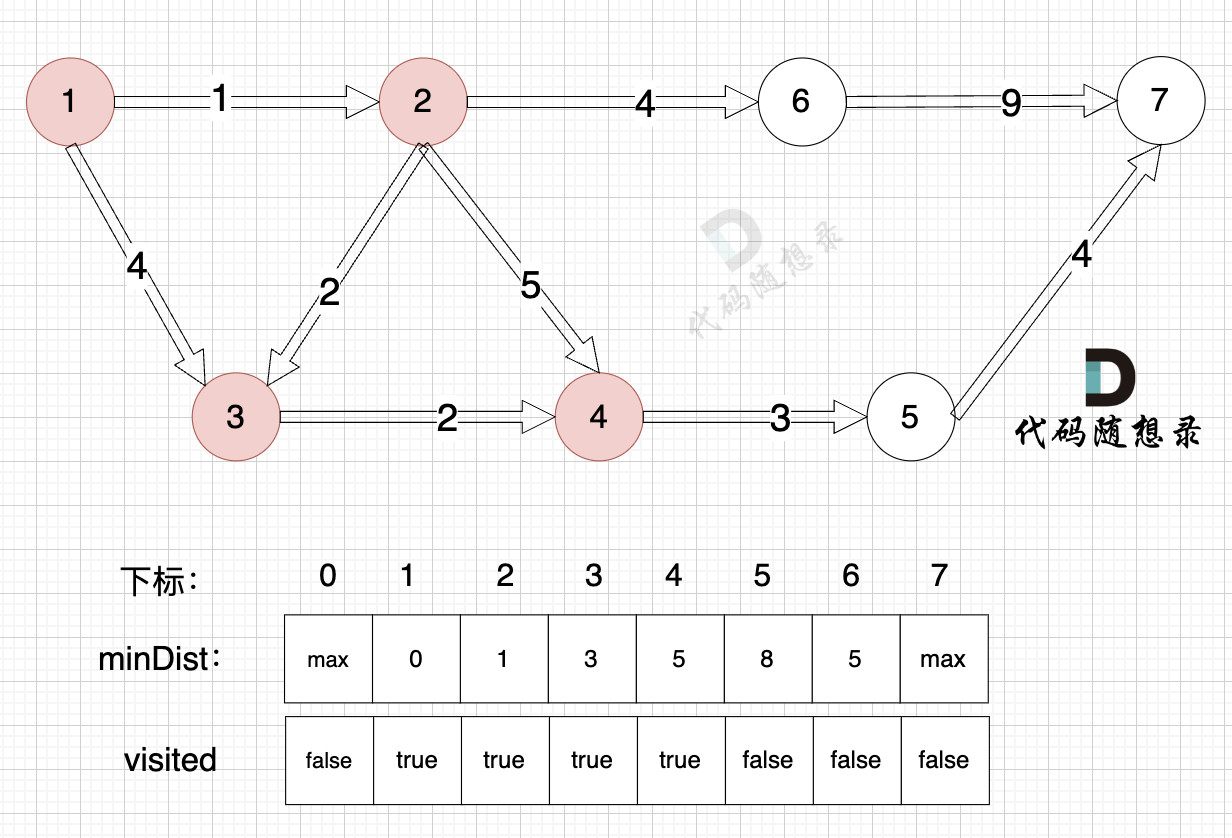
由于节点4的加入，那么源点可以链接到节点5 所以更新minDist数组：

  • 源点到节点5的最短距离为8，小于原minDist[5]的数值max，更新minDist[5] = 8

1、选源点到哪个节点近且该节点未被访问过

距离源点最近且没有被访问过的节点，是节点6，距离源点距离是 5 （minDist[6] = 5）

2、该最近节点被标记访问过

节点6 被标记访问过

3、更新非访问节点到源点的距离（即更新minDist数组） ，如图：

img

img

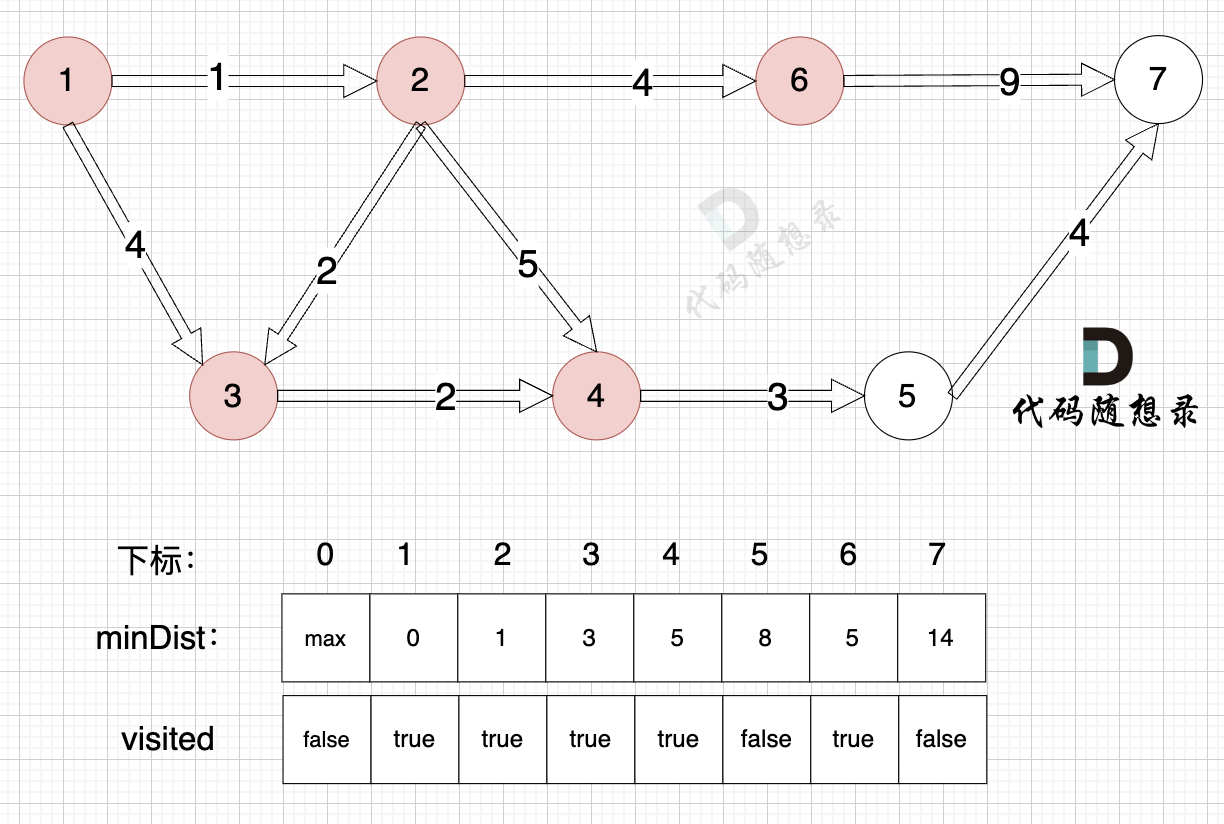
由于节点6的加入，那么源点可以链接到节点7 所以 更新minDist数组：

  • 源点到节点7的最短距离为14，小于原minDist[7]的数值max，更新minDist[7] = 14

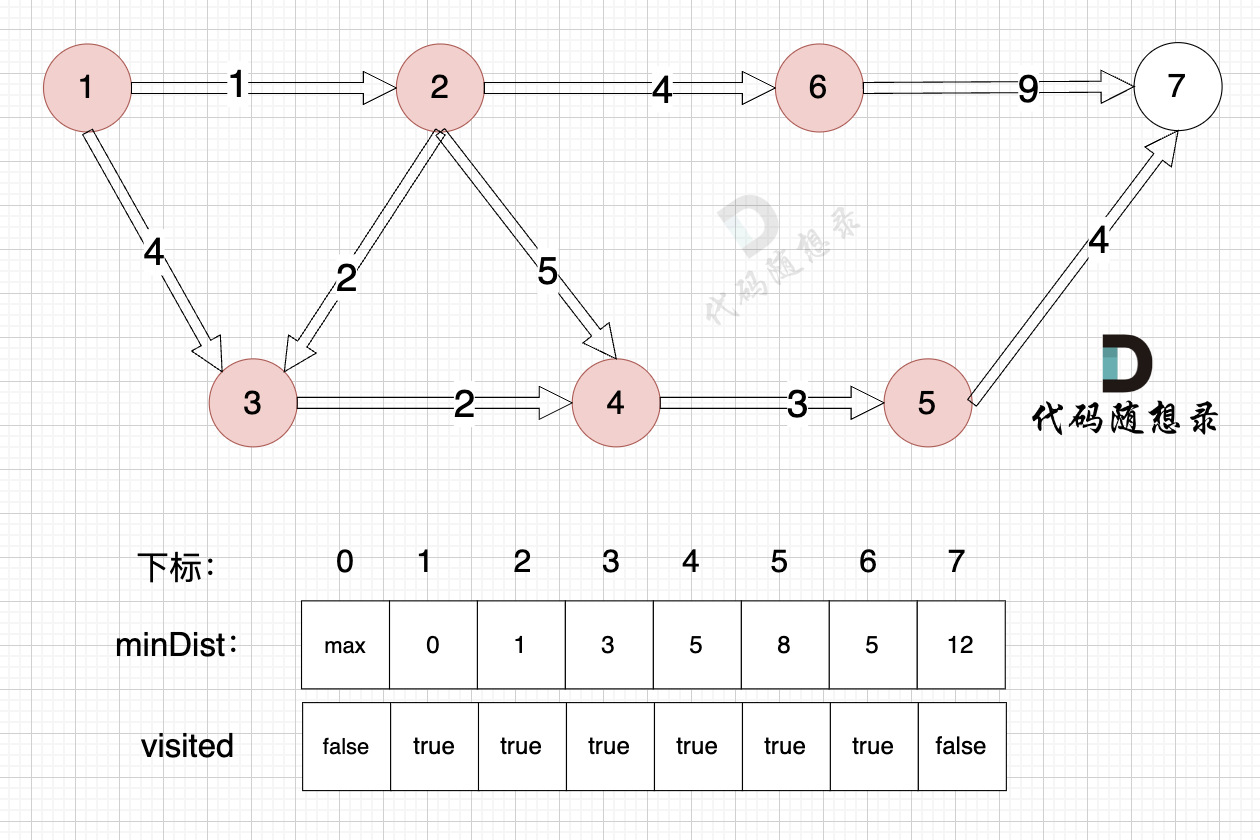
1、选源点到哪个节点近且该节点未被访问过

距离源点最近且没有被访问过的节点，是节点5，距离源点距离是 8 （minDist[5] = 8）

2、该最近节点被标记访问过

节点5 被标记访问过

3、更新非访问节点到源点的距离（即更新minDist数组） ，如图：

img

img

由于节点5的加入，那么源点有新的路径可以链接到节点7 所以 更新minDist数组：

  • 源点到节点7的最短距离为12，小于原minDist[7]的数值14，更新minDist[7] = 12

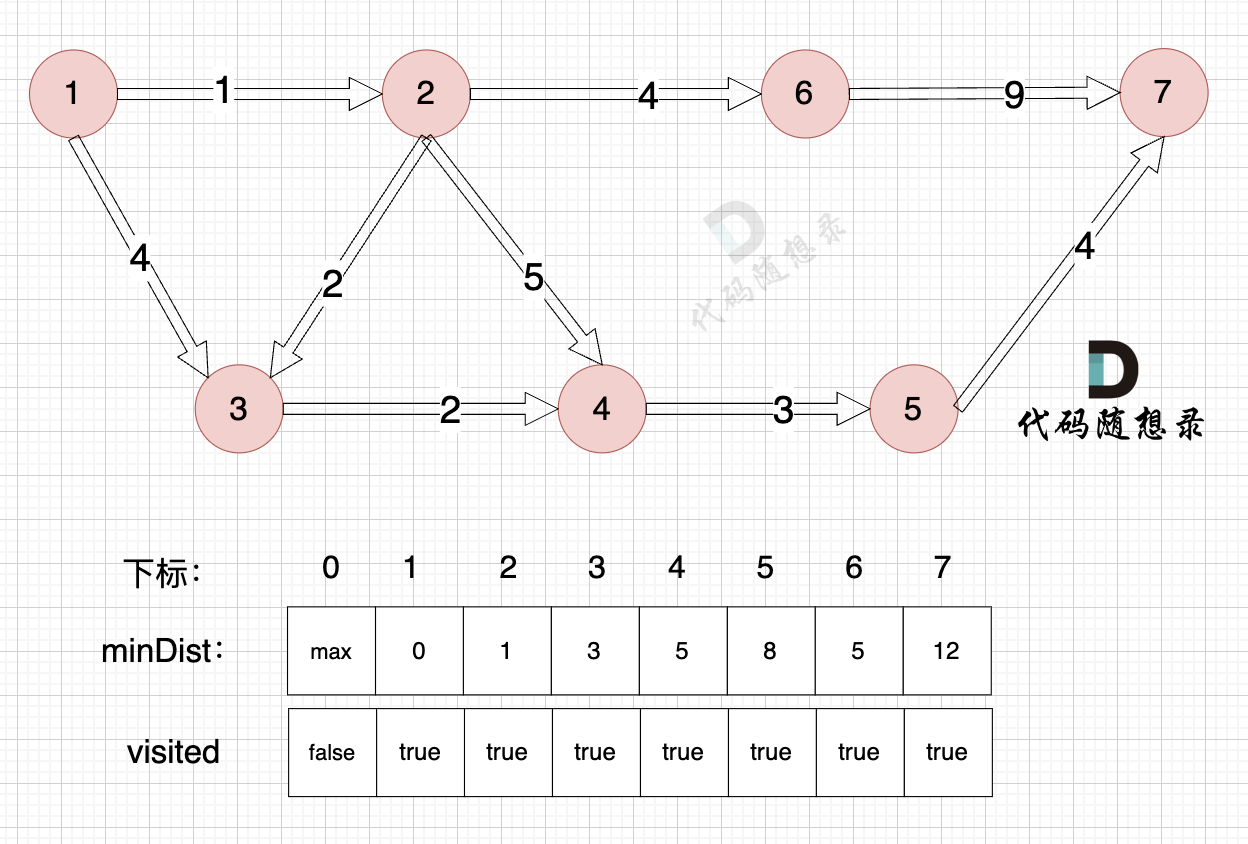
1、选源点到哪个节点近且该节点未被访问过

距离源点最近且没有被访问过的节点，是节点7（终点），距离源点距离是 12 （minDist[7] = 12）

2、该最近节点被标记访问过

节点7 被标记访问过

3、更新非访问节点到源点的距离（即更新minDist数组） ，如图：

img

img

节点7加入，但节点7到节点7的距离为0，所以 不用更新minDist数组

最后我们要求起点（节点1） 到终点 （节点7）的距离。

再来回顾一下minDist数组的含义：记录 每一个节点距离源点的最小距离。

那么起到（节点1）到终点（节点7）的最短距离就是 minDist[7] ，按上面举例讲解来说，minDist[7] = 12，节点1 到节点7的最短路径为 12。

路径如图：

img

img

在上面的讲解中，每一步 我都是按照 dijkstra 三部曲来讲解的，理解了这三部曲，代码也就好懂的

dijkstra代码

  • 时间复杂度O(N2)
  • 空间复杂度O(N2)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
def main():
    n, m = map(int, input().split())

    from collections import defaultdict
    graph = [[float('inf')] * (n + 1) for _ in range(n + 1)]
    graphDict = defaultdict(list)

    for _ in range(m):
        s, t, v = map(int, input().split())
        graph[s][t] = v
        graphDict[s].append(t)

    visited = [0] * (n + 1)
    minDist = [float('inf')] * (n + 1)
    minDist[1] = 0

    parent = [-1] * (n + 1)
    for i in range(n + 1):
        lowest = float('inf')
        node = -1
        for j in range(n + 1):
            if visited[j] == 0 and minDist[j] < lowest:
                lowest = minDist[j]
                node = j
        
        if node == -1:
            break

        visited[node] = 1

        # for t in range(n + 1):  # 在prim算法里，因为prim是全局贪心算法，所以需要对所有节点遍历
        # 而本算法里，只能对node的相邻节点进行遍历
        # 我是使用了graphDict只存储与node相邻的节点
        for t in graphDict[node]:
            if visited[t] == 0 and minDist[t] > graph[node][t]:
                # 在prim算法里，这里会直接等于graph[node][t]
                # prim是求 非访问节点到最小生成树的最小距离，而 dijkstra是求 非访问节点到源点的最小距离。
                # 而本算法，需要判断是否值得更新（graph[node][t] + minDist[node]相当于绕路到node再到t）
                minDist[t] = min(graph[node][t] + minDist[node], minDist[t])
                # parent用来记录边，注意，不能写成parent[node] = t，因为一个node可能会指向多个t，后面的数据会将前面覆盖
                parent[t] = node

        # 或者对n+1遍历，但在条件里添加一个graph[node][t] != float('inf)，达到同样只对node相邻的节点遍历的效果
        # for t in range(n + 1):
        #     if visited[t] == 0 and minDist[t] > graph[node][t] and graph[node][t] != float('inf'):
        #         minDist[t] = min(graph[node][t] + minDist[node], minDist[t])
    
    print(parent)
    print(minDist[-1] if minDist[-1] != float('inf') else -1)
            
    
if __name__ == "__main__":
    main()

dijkstra记录边

初始化一个数组用来记录当前节点的先驱节点

1
parent = [-1] * (n + 1)

在发生数值更新时记录边，注意一定要是parent[t] = node，而不是parent[node] = t，因为一个node可能会对应多个t，后面的数据可能会将前面的覆盖掉

1
2
3
4
for t in graphDict[node]:
    if visited[t] == 0 and minDist[t] > graph[node][t]:
        minDist[t] = min(graph[node][t] + minDist[node], minDist[t])
        parent[t] = node