LeetCodeCapmusR2Day01-数组

第二轮刷题，期望是包含指定任务题目外添加一些额外题目

704. 二分查找

https://leetcode.cn/problems/binary-search/

给定一个 n 个元素有序的（升序）整型数组 nums 和一个目标值 target ，写一个函数搜索 nums 中的 target，如果 target 存在返回下标，否则返回 -1。

你必须编写一个具有 O(log n) 时间复杂度的算法。

示例 1:

1
2
3
输入: nums = [-1,0,3,5,9,12], target = 9
输出: 4
解释: 9 出现在 nums 中并且下标为 4

示例 2:

1
2
3
输入: nums = [-1,0,3,5,9,12], target = 2
输出: -1
解释: 2 不存在 nums 中因此返回 -1

提示：

  1. 你可以假设 nums 中的所有元素是不重复的。
  2. n 将在 [1, 10000]之间。
  3. nums 的每个元素都将在 [-9999, 9999]之间。

代码

  • 时间复杂度O(LogN)
  • 空间复杂度O(1)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
class Solution:
    def search(self, nums: List[int], target: int) -> int:
        left = 0
        L = len(nums)
        right = L - 1

        while left <= right:
            mid = left + (right - left) // 2
            if nums[mid] == target:
                return mid
            elif nums[mid] < target:
                left = mid + 1
            else:
                right = mid - 1
        
        return -1

27. 移除元素

https://leetcode.cn/problems/remove-element/

给你一个数组 nums 和一个值 val，你需要 原地 移除所有数值等于 val 的元素。元素的顺序可能发生改变。然后返回 nums 中与 val 不同的元素的数量。

假设 nums 中不等于 val 的元素数量为 k，要通过此题，您需要执行以下操作：

  • 更改 nums 数组，使 nums 的前 k 个元素包含不等于 val 的元素。nums 的其余元素和 nums 的大小并不重要。
  • 返回 k。

用户评测：

评测机将使用以下代码测试您的解决方案：

1
2
3
4
5
6
7
8
9
10
11
12
int[] nums = [...]; // 输入数组
int val = ...; // 要移除的值
int[] expectedNums = [...]; // 长度正确的预期答案。
                            // 它以不等于 val 的值排序。

int k = removeElement(nums, val); // 调用你的实现

assert k == expectedNums.length;
sort(nums, 0, k); // 排序 nums 的前 k 个元素
for (int i = 0; i < actualLength; i++) {
    assert nums[i] == expectedNums[i];
}

如果所有的断言都通过，你的解决方案将会 通过。

示例 1：

1
2
3
4
输入：nums = [3,2,2,3], val = 3
输出：2, nums = [2,2,_,_]
解释：你的函数函数应该返回 k = 2, 并且 nums 中的前两个元素均为 2。
你在返回的 k 个元素之外留下了什么并不重要（因此它们并不计入评测）。

示例 2：

1
2
3
4
5
输入：nums = [0,1,2,2,3,0,4,2], val = 2
输出：5, nums = [0,1,4,0,3,_,_,_]
解释：你的函数应该返回 k = 5，并且 nums 中的前五个元素为 0,0,1,3,4。
注意这五个元素可以任意顺序返回。
你在返回的 k 个元素之外留下了什么并不重要（因此它们并不计入评测）。

提示：

  • 0 <= nums.length <= 100
  • 0 <= nums[i] <= 50
  • 0 <= val <= 100

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
class Solution:
    def removeElement(self, nums: List[int], val: int) -> int:
        # 使用双指针
        # slow指针指向可以存放数据的，fast遍历每个元素
        slow = 0
        fast = 0
        L = len(nums)
        while fast < L:
            if nums[fast] != val:
                nums[slow] = nums[fast]
                slow += 1
            fast += 1
        return slow

977. 有序数组的平方

https://leetcode.cn/problems/squares-of-a-sorted-array/

给你一个按 非递减顺序 排序的整数数组 nums，返回 每个数字的平方 组成的新数组，要求也按 非递减顺序 排序。

示例 1：

1
2
3
4
输入：nums = [-4,-1,0,3,10]
输出：[0,1,9,16,100]
解释：平方后，数组变为 [16,1,0,9,100]
排序后，数组变为 [0,1,9,16,100]

示例 2：

1
2
输入：nums = [-7,-3,2,3,11]
输出：[4,9,9,49,121]

提示：

  • 1 <= nums.length <= 104
  • -104 <= nums[i] <= 104
  • nums 已按 非递减顺序 排序

进阶：

  • 请你设计时间复杂度为 O(n) 的算法解决本问题

代码

  • 时间复杂度O(N)
  • 空间复杂度O(N)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
class Solution:
    def sortedSquares(self, nums: List[int]) -> List[int]:
        # 最大数只能从最左或最右中产生
        # 使用双指针，left从左向右，right从右向左，每次将nums[left] ^ 2 和nums[right] ^ 2中最大的放在末尾
        left = 0
        L = len(nums)
        right = L - 1
        res = [0] * L
        n = L - 1
        while left <= right:
            numLeftSq = nums[left] ** 2
            numRightSq = nums[right] ** 2
            if numLeftSq < numRightSq:
                res[n] = numRightSq
                right -= 1
            else:
                res[n] = numLeftSq
                left += 1
            n -= 1
        return res

922. 按奇偶排序数组 II

https://leetcode.cn/problems/sort-array-by-parity-ii/

给定一个非负整数数组 nums， nums 中一半整数是 奇数 ，一半整数是 偶数 。

对数组进行排序，以便当 nums[i] 为奇数时，i 也是 奇数 ；当 nums[i] 为偶数时， i 也是 偶数 。

你可以返回 任何满足上述条件的数组作为答案 。

示例 1：

1
2
3
输入：nums = [4,2,5,7]
输出：[4,5,2,7]
解释：[4,7,2,5]，[2,5,4,7]，[2,7,4,5] 也会被接受。

示例 2：

1
2
输入：nums = [2,3]
输出：[2,3]

提示：

  • 2 <= nums.length <= 2 * 104
  • nums.length 是偶数
  • nums 中一半是偶数
  • 0 <= nums[i] <= 1000

**进阶：**可以不使用额外空间解决问题吗

代码

  • 时间复杂度O(N)
  • 这里时间复杂度并不是O(n^2)，因为偶数位和奇数位都只操作一次，不是n/2 * n/2的关系，而是n/2 + n/2的关系！
  • 空间复杂度O(1)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
class Solution:
    def sortArrayByParityII(self, nums: List[int]) -> List[int]:
        # 使用三指针
        # odd指针记录奇数可以放在的位置
        # i指针用来遍历每个数字

        odd = 1
        L = len(nums)

        for i in range(0, L, 2):
            # 偶数位遇到奇数
            if nums[i] % 2 == 1:
                # 在奇数位找个偶数
                while nums[odd] % 2 !=0:
                    odd += 2
                if nums[odd]!= nums[i]:
                    # 交换
                    nums[odd] ^= nums[i]
                    nums[i] ^= nums[odd]
                    nums[odd] ^= nums[i]

        return nums

35. 搜索插入位置

https://leetcode.cn/problems/search-insert-position/

给定一个排序数组和一个目标值，在数组中找到目标值，并返回其索引。如果目标值不存在于数组中，返回它将会被按顺序插入的位置。

请必须使用时间复杂度为 O(log n) 的算法。

示例 1:

1
2
输入: nums = [1,3,5,6], target = 5
输出: 2

示例 2:

1
2
输入: nums = [1,3,5,6], target = 2
输出: 1

示例 3:

1
2
输入: nums = [1,3,5,6], target = 7
输出: 4

提示:

  • 1 <= nums.length <= 104
  • -104 <= nums[i] <= 104
  • nums 为 无重复元素 的 升序 排列数组
  • -104 <= target <= 104

代码

  • 时间复杂度O(logN)
  • 空间复杂度O(1)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
class Solution:
    def findLeftBorder(self, nums: List[int], target: int) -> int:
        left = 0
        L = len(nums)
        right = L - 1
        while left <= right:
            mid = left + (right - left) // 2
            if nums[mid] == target:
                return mid
            elif nums[mid] < target:
                left = mid + 1
            else:
                # 一旦发现大于或者等于target的num[mid]，那么i就是我们要的结果
                right = mid - 1
        
        return right + 1

    def searchInsert(self, nums: List[int], target: int) -> int:
        res = self.findLeftBorder(nums, target)
        return int(res)

41. 缺失的第一个正数

https://leetcode.cn/problems/first-missing-positive/

给你一个未排序的整数数组 nums ，请你找出其中没有出现的最小的正整数。

请你实现时间复杂度为 O(n) 并且只使用常数级别额外空间的解决方案。

示例 1：

1
2
3
输入：nums = [1,2,0]
输出：3
解释：范围 [1,2] 中的数字都在数组中。

示例 2：

1
2
3
输入：nums = [3,4,-1,1]
输出：2
解释：1 在数组中，但 2 没有。

示例 3：

1
2
3
输入：nums = [7,8,9,11,12]
输出：1
解释：最小的正数 1 没有出现。

提示：

  • 1 <= nums.length <= 105
  • -231 <= nums[i] <= 231 - 1

一般思路

可以从1开始依次枚举正整数，并且遍历数组；但这样的时间复杂度为O(N^2)，空间复杂度为O(1)；

当然，可以使用hashtable，将时间复杂度降到O(N)，但空间复杂度会为O(N)；因为hashtable的查找时间是O(1)。我们为什么要使用哈希表？这是因为哈希表是一个可以支持快速查找的数据结构：给定一个元素，我们可以在 *O*(1) 的时间查找该元素是否在哈希表中

进阶思路

可以先将数组排序，然后对数据进行遍历，所有0以及负数可以不管，再按正数顺序查找数组中可以达到的不存在的最小正数;

但这个对数组排序仍然会占用更多空间

进阶思路代码

  • 时间复杂度O(N)
  • 空间复杂度O(N) # 对数组排序需要占用空间
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class Solution:
    def firstMissingPositive(self, nums: List[int]) -> int:
        # 所有0以及负数都可以不管，重复值可以不管
        # 先排序一遍，再按顺序找不存在的数
        nums.sort()

        L = len(nums)
        # 设置个positive，假设从1开始
        positive = 1
        for i in range(L):
            if nums[i] <= 0:
                continue
            # 如果遍历到positive则说明最小的正数不是当前值，可以找下一个
            if nums[i] == positive:
                positive += 1
            # 提前退出
            if nums[i] > positive:
                break
        return positive

动脑筋思路

那是否有什么方法，允许对nums数组进行修改，并且保持O(N)的时间复杂度呢？

本题目如果是有序的数组，那就很好解决了，但问题就出在现在是无序的；

下面有个不错的思路：

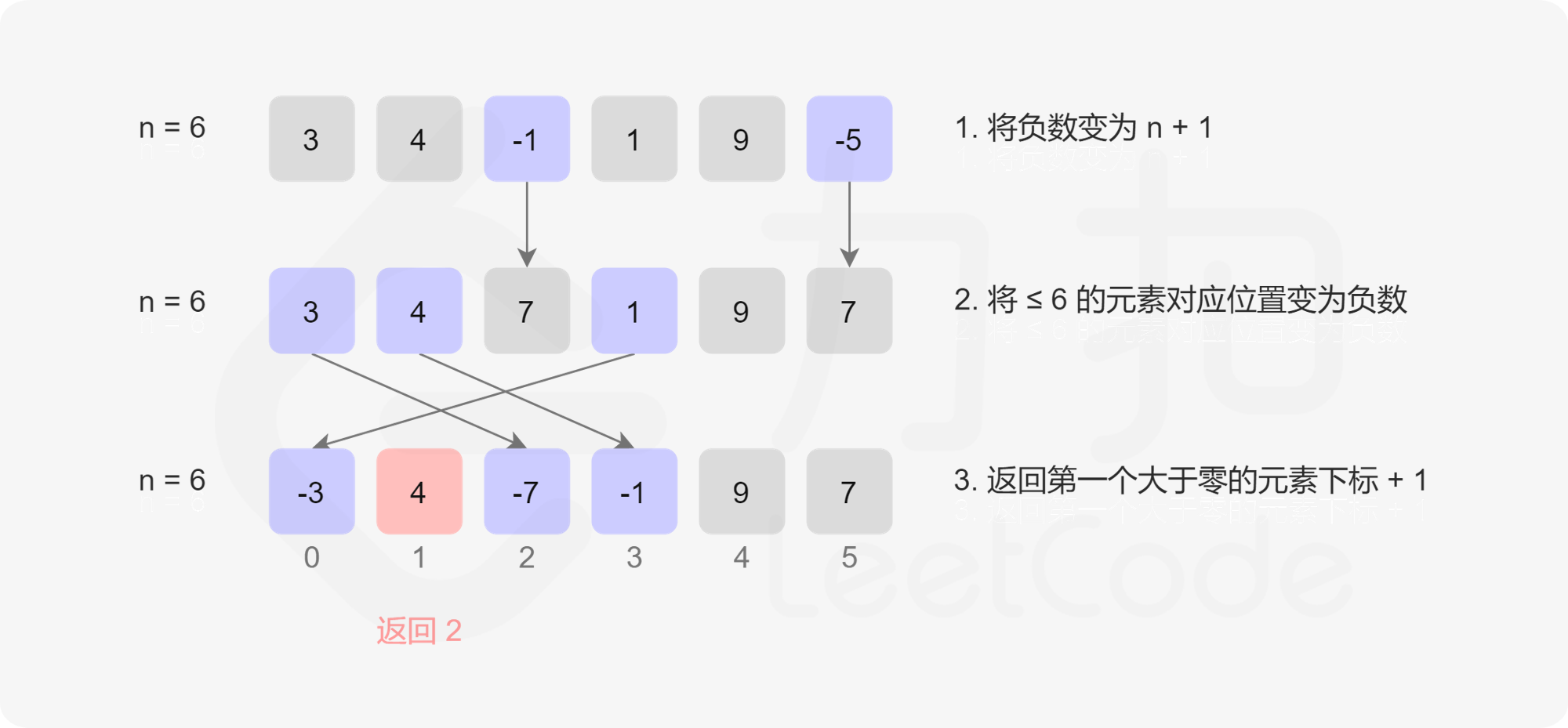
题目要求一个长度为N的数组，所以没有出现的最小正整数的范围一定是[1, N + 1]（都是闭区间），我们对数组进行遍历，对于遍历到的数x，如果它在[1, N]范围内，则将数组中的第x - 1位置（因为下标从0开始）打上标记，如果在遍历结果后，所有位置都被打了标记，则说明最小正整数是N+1；否则，最小正整数就是没有标记的下标+1

比如n = 6

3 4 -1 1 9 -5 1.将负数变为n+1
3 4 7 1 9 7 2.将小于n=6的元素，它对应位置变成负数
-3 4 -7 -1 9 7 3.返回第一个大于0的下标+1

注意，这里的第二步：将小于n=6的元素，它对应位置变成负数

比如第一个元素3，则将nums[3 - 1] = -abs(nums[3 - 1])，那就是将下标为2的原元素7变成1了-7

比如元素1，则将nums[1 - 1] = -abs(nums[1 - 1])，将下标为0的原元素3变成了-3

也就是说，如果某个正数在数组里出现了，那把这个正数当作下标，将下标所在的数字打上标记（这里是将其值设置为负数）

比如下图中，缺少正数2，所以下标nums[2 - 1]的数字不会被打上标记！最终我们只要找哪个数字没有标记！它的下标就是我们要找的最小正数

下面这个图看得更清楚

image-20250903142618235

img